Question Number 78794 by naka3546 last updated on 20/Jan/20
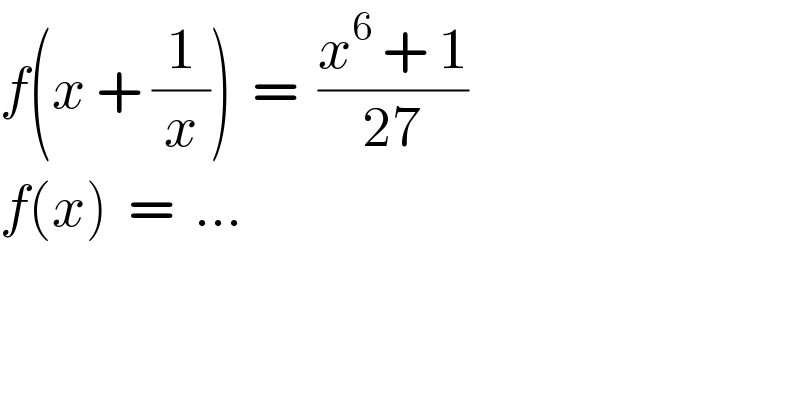
$${f}\left({x}\:+\:\frac{\mathrm{1}}{{x}}\right)\:\:=\:\:\frac{{x}^{\mathrm{6}} \:+\:\mathrm{1}}{\mathrm{27}} \\ $$$${f}\left({x}\right)\:\:=\:\:… \\ $$
Answered by mr W last updated on 20/Jan/20
![t=x+(1/x) x^2 −tx+1=0 ⇒x=(1/2)(t±(√(t^2 −4))) x^2 =tx−1 x^3 =tx^2 −x=t(tx−1)−x=(t^2 −1)x−t x^6 =(t^2 −1)^2 x^2 −2t(t^2 −1)x+t^2 x^6 =(t^2 −1)^2 (tx−1)−2t(t^2 −1)x+t^2 x^6 =t(t^2 −3)[(t^2 −1)x−t]−1 x^6 +1=t(t^2 −3)[(t^2 −1)x−t] ((x^6 +1)/(27))=((t(t^2 −3))/(27))[(((t^2 −1)(t±(√(t^2 −4))))/2)−t] f(t)=((t(t^2 −3))/(27))[(((t^2 −1)(t±(√(t^2 −4))))/2)−t] ⇒f(x)=((x(x^2 −3))/(27))[(((x^2 −1)(x±(√(x^2 −4))))/2)−x]](https://www.tinkutara.com/question/Q78798.png)
$${t}={x}+\frac{\mathrm{1}}{{x}} \\ $$$${x}^{\mathrm{2}} −{tx}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{2}}\left({t}\pm\sqrt{{t}^{\mathrm{2}} −\mathrm{4}}\right) \\ $$$${x}^{\mathrm{2}} ={tx}−\mathrm{1} \\ $$$${x}^{\mathrm{3}} ={tx}^{\mathrm{2}} −{x}={t}\left({tx}−\mathrm{1}\right)−{x}=\left({t}^{\mathrm{2}} −\mathrm{1}\right){x}−{t} \\ $$$${x}^{\mathrm{6}} =\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} {x}^{\mathrm{2}} −\mathrm{2}{t}\left({t}^{\mathrm{2}} −\mathrm{1}\right){x}+{t}^{\mathrm{2}} \\ $$$${x}^{\mathrm{6}} =\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \left({tx}−\mathrm{1}\right)−\mathrm{2}{t}\left({t}^{\mathrm{2}} −\mathrm{1}\right){x}+{t}^{\mathrm{2}} \\ $$$${x}^{\mathrm{6}} ={t}\left({t}^{\mathrm{2}} −\mathrm{3}\right)\left[\left({t}^{\mathrm{2}} −\mathrm{1}\right){x}−{t}\right]−\mathrm{1} \\ $$$${x}^{\mathrm{6}} +\mathrm{1}={t}\left({t}^{\mathrm{2}} −\mathrm{3}\right)\left[\left({t}^{\mathrm{2}} −\mathrm{1}\right){x}−{t}\right] \\ $$$$\frac{{x}^{\mathrm{6}} +\mathrm{1}}{\mathrm{27}}=\frac{{t}\left({t}^{\mathrm{2}} −\mathrm{3}\right)}{\mathrm{27}}\left[\frac{\left({t}^{\mathrm{2}} −\mathrm{1}\right)\left({t}\pm\sqrt{{t}^{\mathrm{2}} −\mathrm{4}}\right)}{\mathrm{2}}−{t}\right] \\ $$$${f}\left({t}\right)=\frac{{t}\left({t}^{\mathrm{2}} −\mathrm{3}\right)}{\mathrm{27}}\left[\frac{\left({t}^{\mathrm{2}} −\mathrm{1}\right)\left({t}\pm\sqrt{{t}^{\mathrm{2}} −\mathrm{4}}\right)}{\mathrm{2}}−{t}\right] \\ $$$$\Rightarrow{f}\left({x}\right)=\frac{{x}\left({x}^{\mathrm{2}} −\mathrm{3}\right)}{\mathrm{27}}\left[\frac{\left({x}^{\mathrm{2}} −\mathrm{1}\right)\left({x}\pm\sqrt{{x}^{\mathrm{2}} −\mathrm{4}}\right)}{\mathrm{2}}−{x}\right] \\ $$
