Question Number 117518 by bobhans last updated on 12/Oct/20
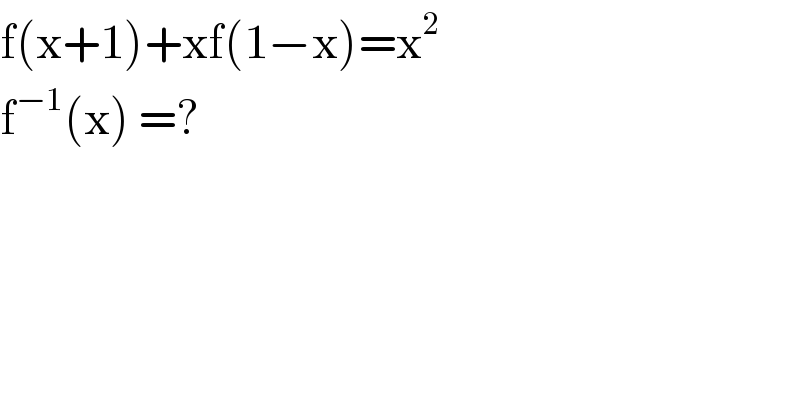
$$\mathrm{f}\left(\mathrm{x}+\mathrm{1}\right)+\mathrm{xf}\left(\mathrm{1}−\mathrm{x}\right)=\mathrm{x}^{\mathrm{2}} \\ $$$$\mathrm{f}^{−\mathrm{1}} \left(\mathrm{x}\right)\:=? \\ $$
Answered by bemath last updated on 12/Oct/20
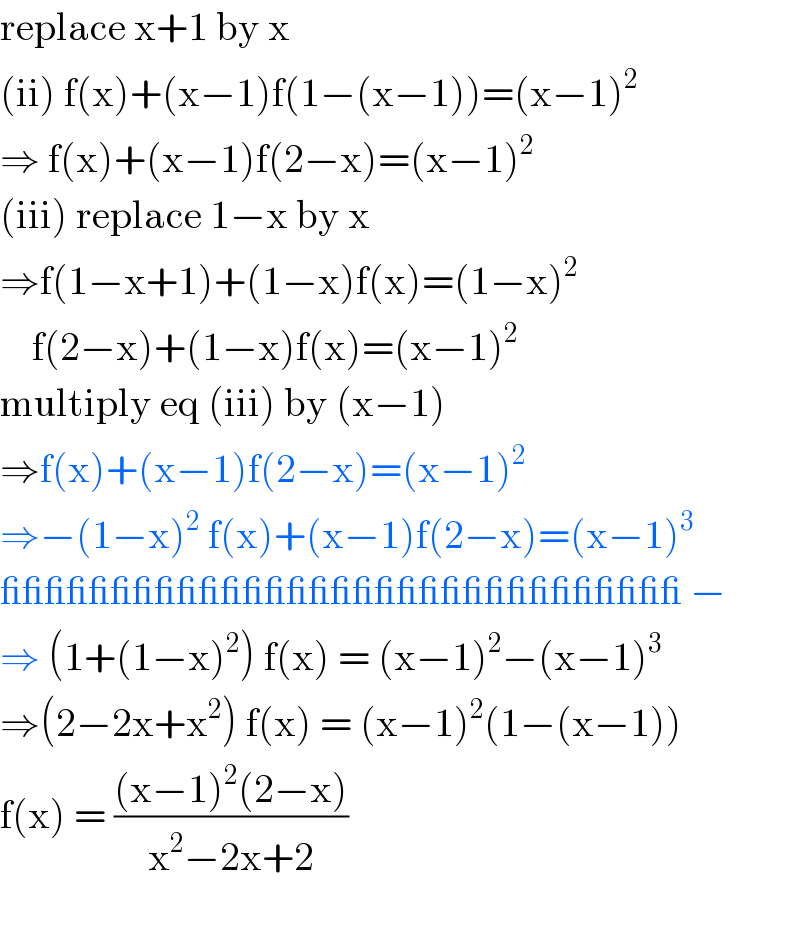
$$\mathrm{replace}\:\mathrm{x}+\mathrm{1}\:\mathrm{by}\:\mathrm{x} \\ $$$$\left(\mathrm{ii}\right)\:\mathrm{f}\left(\mathrm{x}\right)+\left(\mathrm{x}−\mathrm{1}\right)\mathrm{f}\left(\mathrm{1}−\left(\mathrm{x}−\mathrm{1}\right)\right)=\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{f}\left(\mathrm{x}\right)+\left(\mathrm{x}−\mathrm{1}\right)\mathrm{f}\left(\mathrm{2}−\mathrm{x}\right)=\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{iii}\right)\:\mathrm{replace}\:\mathrm{1}−\mathrm{x}\:\mathrm{by}\:\mathrm{x} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{1}−\mathrm{x}+\mathrm{1}\right)+\left(\mathrm{1}−\mathrm{x}\right)\mathrm{f}\left(\mathrm{x}\right)=\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\mathrm{f}\left(\mathrm{2}−\mathrm{x}\right)+\left(\mathrm{1}−\mathrm{x}\right)\mathrm{f}\left(\mathrm{x}\right)=\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{multiply}\:\mathrm{eq}\:\left(\mathrm{iii}\right)\:\mathrm{by}\:\left(\mathrm{x}−\mathrm{1}\right) \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)+\left(\mathrm{x}−\mathrm{1}\right)\mathrm{f}\left(\mathrm{2}−\mathrm{x}\right)=\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow−\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} \:\mathrm{f}\left(\mathrm{x}\right)+\left(\mathrm{x}−\mathrm{1}\right)\mathrm{f}\left(\mathrm{2}−\mathrm{x}\right)=\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{3}} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\:− \\ $$$$\Rightarrow\:\left(\mathrm{1}+\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} \right)\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} −\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{3}} \\ $$$$\Rightarrow\left(\mathrm{2}−\mathrm{2x}+\mathrm{x}^{\mathrm{2}} \right)\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{1}−\left(\mathrm{x}−\mathrm{1}\right)\right) \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\:\frac{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{2}−\mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{2}} \\ $$$$ \\ $$
