Menu Close

f-x-2-1-sinx-2-developp-f-at-fourier-serie-

Tinku Tara 0 Comments
Pin




Question Number 144464 by mathmax by abdo last updated on 25/Jun/21
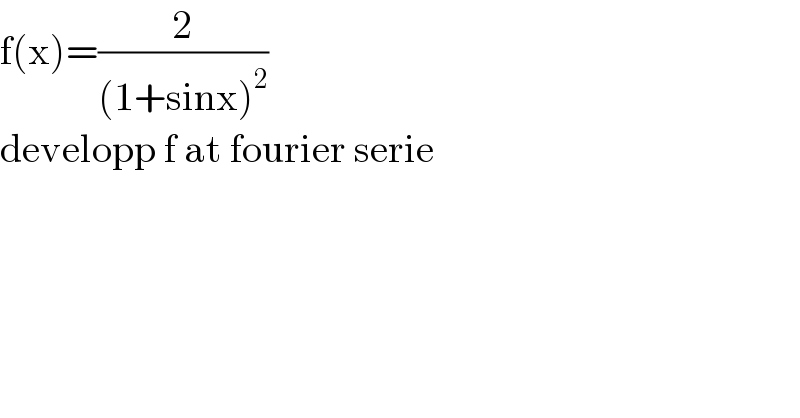
f(x)=(2/((1+sinx)^2 )) developp f at fourier serie
$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{2}}{\left(\mathrm{1}+\mathrm{sinx}\right)^{\mathrm{2}} } \\ $$$$\mathrm{developp}\:\mathrm{f}\:\mathrm{at}\:\mathrm{fourier}\:\mathrm{serie} \\ $$
Answered by mathmax by abdo last updated on 26/Jun/21
let f(a)=(2/(a+sinx)) ⇒f^′ (a)=−(2/((a+sinx)^2 )) ⇒−f^′ (1)=(2/((1+sinx)^2 )) we have f(a)=(2/(a+((e^(ix) −e^(−ix) )/(2i))))=((4i)/(2ia+e^(ix) −e^(−ix) )) =_(e^(ix) =z) ((4i)/(2ia+z−z^(−1) ))=((4iz)/(2iaz+z^2 −1))=((4iz)/(z^2 +2iaz −1)) Δ^′ =−a^2 +1 =1−a^2 ⇒z_1 =−ia+(√(1−a^2 )) z_2 =−ia−(√(1−a^2 )) ⇒f(a)=((4iz)/((z−z_1 )(z−z_2 ))) =4iz((1/(z−z_1 ))−(1/(z−z_2 ))).(1/(z_1 −z_2 ))=((4i)/(2(√(1−a^2 ))))((z/(z−z_1 ))−(z/(z−z_2 ))) ∣(z/z_1 )∣=1 and ∣(z/z_2 )∣=1 ⇒f(a)=((2i)/( (√(1−a^2 ))))((z/(z_1 ((z/z_1 )−1)))−(z/(z_2 ((z/z_2 )−1)))) =((2iz)/( (√(1−a^2 ))))((1/(1−(z/z_2 )))−(1/(1−(z/z_1 ))))=((2iz)/( (√(1−a^2 ))))(Σ_(n=0) ^∞ (z^n /z_2 ^n )−Σ_(n=0) ^∞ (z^n /z_1 ^n )) z_1 =e^(iarctan(−(a/( (√(1−a^2 )))))) and z_2 =e^(iarctan((a/( (√(1−a^2 )))))) ⇒ ⇒(1/z_1 ^n )=e^(inarctan((a/( (√(1−a^2 )))))) +e^(−inarctan((a/( (√(1−a^2 )))))) =2Re(....) =2cos(narctan((a/( (√(1−a^2 )))))) ⇒ f(a)=((2iz)/( (√(1−a^2 ))))Σ_(n=0) ^∞ 2cos(narctan((a/( (√(1−a^2 ))))))e^(inx) =((4i)/( (√(1−a^2 ))))Σ_(n=0) ^∞ cos(narctan((a/( (√(1−a^2 ))))))(cos(n+1)x+isin(n+1)x) =4i(....)−(4/( (√(1−a^2 ))))Σ_(n=0) ^∞ cos(narctan((a/( (√(1−a^2 ))))))sin(n+1)x f(a) is reaal ⇒ f(a)=((−4)/( (√(1−a^2 ))))Σ_(n=0) ^∞ cos(narctan((a/( (√(1−a^2 ))))))sin(n+1)x rest to calculate f^′ (a)....be continued
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)=\frac{\mathrm{2}}{\mathrm{a}+\mathrm{sinx}}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{a}\right)=−\frac{\mathrm{2}}{\left(\mathrm{a}+\mathrm{sinx}\right)^{\mathrm{2}} }\:\Rightarrow−\mathrm{f}^{'} \left(\mathrm{1}\right)=\frac{\mathrm{2}}{\left(\mathrm{1}+\mathrm{sinx}\right)^{\mathrm{2}} } \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{f}\left(\mathrm{a}\right)=\frac{\mathrm{2}}{\mathrm{a}+\frac{\mathrm{e}^{\mathrm{ix}} −\mathrm{e}^{−\mathrm{ix}} }{\mathrm{2i}}}=\frac{\mathrm{4i}}{\mathrm{2ia}+\mathrm{e}^{\mathrm{ix}} −\mathrm{e}^{−\mathrm{ix}} } \\ $$$$=_{\mathrm{e}^{\mathrm{ix}} \:=\mathrm{z}} \:\:\:\frac{\mathrm{4i}}{\mathrm{2ia}+\mathrm{z}−\mathrm{z}^{−\mathrm{1}} }=\frac{\mathrm{4iz}}{\mathrm{2iaz}+\mathrm{z}^{\mathrm{2}} −\mathrm{1}}=\frac{\mathrm{4iz}}{\mathrm{z}^{\mathrm{2}} \:+\mathrm{2iaz}\:−\mathrm{1}} \\ $$$$\Delta^{'} =−\mathrm{a}^{\mathrm{2}} +\mathrm{1}\:=\mathrm{1}−\mathrm{a}^{\mathrm{2}} \:\Rightarrow\mathrm{z}_{\mathrm{1}} =−\mathrm{ia}+\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} } \\ $$$$\mathrm{z}_{\mathrm{2}} =−\mathrm{ia}−\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }\:\:\Rightarrow\mathrm{f}\left(\mathrm{a}\right)=\frac{\mathrm{4iz}}{\left(\mathrm{z}−\mathrm{z}_{\mathrm{1}} \right)\left(\mathrm{z}−\mathrm{z}_{\mathrm{2}} \right)} \\ $$$$=\mathrm{4iz}\left(\frac{\mathrm{1}}{\mathrm{z}−\mathrm{z}_{\mathrm{1}} }−\frac{\mathrm{1}}{\mathrm{z}−\mathrm{z}_{\mathrm{2}} }\right).\frac{\mathrm{1}}{\mathrm{z}_{\mathrm{1}} −\mathrm{z}_{\mathrm{2}} }=\frac{\mathrm{4i}}{\mathrm{2}\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}\left(\frac{\mathrm{z}}{\mathrm{z}−\mathrm{z}_{\mathrm{1}} }−\frac{\mathrm{z}}{\mathrm{z}−\mathrm{z}_{\mathrm{2}} }\right) \\ $$$$\mid\frac{\mathrm{z}}{\mathrm{z}_{\mathrm{1}} }\mid=\mathrm{1}\:\:\mathrm{and}\:\mid\frac{\mathrm{z}}{\mathrm{z}_{\mathrm{2}} }\mid=\mathrm{1}\:\Rightarrow\mathrm{f}\left(\mathrm{a}\right)=\frac{\mathrm{2i}}{\:\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}\left(\frac{\mathrm{z}}{\mathrm{z}_{\mathrm{1}} \left(\frac{\mathrm{z}}{\mathrm{z}_{\mathrm{1}} }−\mathrm{1}\right)}−\frac{\mathrm{z}}{\mathrm{z}_{\mathrm{2}} \left(\frac{\mathrm{z}}{\mathrm{z}_{\mathrm{2}} }−\mathrm{1}\right)}\right) \\ $$$$=\frac{\mathrm{2iz}}{\:\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}\left(\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{z}}{\mathrm{z}_{\mathrm{2}} }}−\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{z}}{\mathrm{z}_{\mathrm{1}} }}\right)=\frac{\mathrm{2iz}}{\:\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}\left(\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{z}^{\mathrm{n}} }{\mathrm{z}_{\mathrm{2}} ^{\mathrm{n}} }−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{z}^{\mathrm{n}} }{\mathrm{z}_{\mathrm{1}} ^{\mathrm{n}} }\right) \\ $$$$\mathrm{z}_{\mathrm{1}} =\mathrm{e}^{\mathrm{iarctan}\left(−\frac{\mathrm{a}}{\:\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}\right)} \:\mathrm{and}\:\mathrm{z}_{\mathrm{2}} =\mathrm{e}^{\mathrm{iarctan}\left(\frac{\mathrm{a}}{\:\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}\right)} \:\Rightarrow \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{z}_{\mathrm{1}} ^{\mathrm{n}} }=\mathrm{e}^{\mathrm{inarctan}\left(\frac{\mathrm{a}}{\:\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}\right)} +\mathrm{e}^{−\mathrm{inarctan}\left(\frac{\mathrm{a}}{\:\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}\right)} =\mathrm{2Re}\left(….\right) \\ $$$$=\mathrm{2cos}\left(\mathrm{narctan}\left(\frac{\mathrm{a}}{\:\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}\right)\right)\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\frac{\mathrm{2iz}}{\:\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{2cos}\left(\mathrm{narctan}\left(\frac{\mathrm{a}}{\:\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}\right)\right)\mathrm{e}^{\mathrm{inx}} \\ $$$$=\frac{\mathrm{4i}}{\:\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{cos}\left(\mathrm{narctan}\left(\frac{\mathrm{a}}{\:\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}\right)\right)\left(\mathrm{cos}\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}+\mathrm{isin}\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}\right) \\ $$$$=\mathrm{4i}\left(….\right)−\frac{\mathrm{4}}{\:\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{cos}\left(\mathrm{narctan}\left(\frac{\mathrm{a}}{\:\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}\right)\right)\mathrm{sin}\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x} \\ $$$$\mathrm{f}\left(\mathrm{a}\right)\:\mathrm{is}\:\mathrm{reaal}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\frac{−\mathrm{4}}{\:\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{cos}\left(\mathrm{narctan}\left(\frac{\mathrm{a}}{\:\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}\right)\right)\mathrm{sin}\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x} \\ $$$$\mathrm{rest}\:\mathrm{to}\:\mathrm{calculate}\:\mathrm{f}^{'} \left(\mathrm{a}\right)….\mathrm{be}\:\mathrm{continued} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *