Question Number 23833 by Joel577 last updated on 07/Nov/17
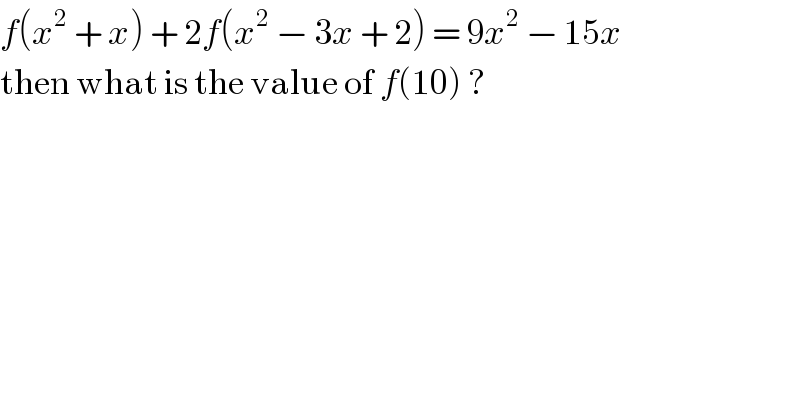
$${f}\left({x}^{\mathrm{2}} \:+\:{x}\right)\:+\:\mathrm{2}{f}\left({x}^{\mathrm{2}} \:−\:\mathrm{3}{x}\:+\:\mathrm{2}\right)\:=\:\mathrm{9}{x}^{\mathrm{2}} \:−\:\mathrm{15}{x} \\ $$$$\mathrm{then}\:\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{f}\left(\mathrm{10}\right)\:? \\ $$
Commented by prakash jain last updated on 07/Nov/17
![x=0 f(0)+2f(2)=0 x=1 f(2)+2f(0)=−6 f(2)=2 f(0)=−4 f(x) is linear function f(x)=ax+b ⇒f(x)=3x−4 f(x^2 +x)+2f(x^2 −3x+2)= =3(x^2 +x)−4+2[3(x^2 −3x+2)−4] =3x^2 +3x−4+2(3x^2 −9x+2) =9x^2 −15x f(x)=3x−4 f(10) =30−4=26](https://www.tinkutara.com/question/Q23843.png)
$${x}=\mathrm{0} \\ $$$${f}\left(\mathrm{0}\right)+\mathrm{2}{f}\left(\mathrm{2}\right)=\mathrm{0} \\ $$$${x}=\mathrm{1} \\ $$$${f}\left(\mathrm{2}\right)+\mathrm{2}{f}\left(\mathrm{0}\right)=−\mathrm{6} \\ $$$${f}\left(\mathrm{2}\right)=\mathrm{2} \\ $$$${f}\left(\mathrm{0}\right)=−\mathrm{4} \\ $$$${f}\left({x}\right)\:\mathrm{is}\:\mathrm{linear}\:\mathrm{function} \\ $$$${f}\left({x}\right)={ax}+{b} \\ $$$$\Rightarrow{f}\left({x}\right)=\mathrm{3}{x}−\mathrm{4} \\ $$$${f}\left({x}^{\mathrm{2}} +{x}\right)+\mathrm{2}{f}\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}\right)= \\ $$$$=\mathrm{3}\left({x}^{\mathrm{2}} +{x}\right)−\mathrm{4}+\mathrm{2}\left[\mathrm{3}\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}\right)−\mathrm{4}\right] \\ $$$$=\mathrm{3}{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{4}+\mathrm{2}\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{9}{x}+\mathrm{2}\right) \\ $$$$=\mathrm{9}{x}^{\mathrm{2}} −\mathrm{15}{x} \\ $$$${f}\left({x}\right)=\mathrm{3}{x}−\mathrm{4} \\ $$$${f}\left(\mathrm{10}\right) \\ $$$$=\mathrm{30}−\mathrm{4}=\mathrm{26} \\ $$
Commented by ajfour last updated on 07/Nov/17
$${you}\:{make}\:{it}\:{easy}\:{enough}\:{sir}! \\ $$
Commented by Joel577 last updated on 08/Nov/17
$${thank}\:{you}\:{very}\:{much} \\ $$
Answered by kaivan.ahmadi last updated on 13/Dec/17

$$\mathrm{f}\left(\mathrm{0}\right)=−\mathrm{4}\:\:\:\mathrm{az}\:\mathrm{the}\:\mathrm{Mr}\:\mathrm{parkash}\:\mathrm{slution} \\ $$$$\mathrm{if}\:\mathrm{we}\:\mathrm{set}\:\mathrm{x}^{\mathrm{2}} +\mathrm{x}=\mathrm{10}\Rightarrow \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{2}=−\mathrm{4x}+\mathrm{12} \\ $$$$\mathrm{and} \\ $$$$\mathrm{9x}^{\mathrm{2}} −\mathrm{15x}=−\mathrm{24x}+\mathrm{90} \\ $$$$\mathrm{Now}\:\mathrm{replace} \\ $$$$\mathrm{f}\left(\mathrm{10}\right)+\mathrm{2f}\left(−\mathrm{4x}+\mathrm{12}\right)=−\mathrm{24x}+\mathrm{90} \\ $$$$\mathrm{and}\:\mathrm{so}\:\mathrm{for}\:\mathrm{x}=\mathrm{3}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{f}\left(\mathrm{10}\right)+\mathrm{2f}\left(\mathrm{0}\right)=\mathrm{18}\Rightarrow\mathrm{f}\left(\mathrm{10}\right)=\mathrm{26} \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{way}\:\mathrm{we}\:\mathrm{didnt}\:\mathrm{use}\:\mathrm{the} \\ $$$$\mathrm{linearly}\:\mathrm{of}\:\:\:\mathrm{f}. \\ $$$$ \\ $$
Commented by prakash jain last updated on 13/Dec/17

$$\mathrm{Thanks}.\:\mathrm{It}\:\mathrm{is}\:\mathrm{a}\:\mathrm{good}\:\mathrm{approach}. \\ $$$$\mathrm{Very}\:\mathrm{useful}\:\mathrm{when}\:\mathrm{it}\:\mathrm{is}\:\mathrm{difficult} \\ $$$$\mathrm{to}\:\mathrm{evaluate}\:{f}\left({x}\right)\:\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:{x}\:\mathrm{alone}. \\ $$
