Menu Close

f-x-2arctan-1-x-x-f-x-

Tinku Tara 0 Comments
Pin




Question Number 39949 by zesearho last updated on 13/Jul/18
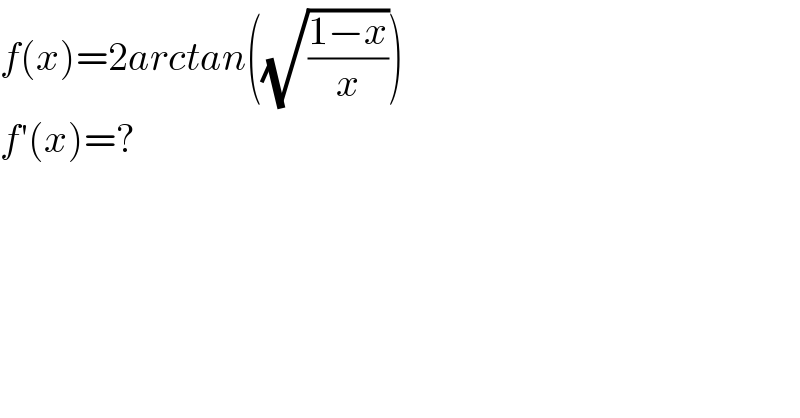
f(x)=2arctan((√((1−x)/x))) f′(x)=?
$${f}\left({x}\right)=\mathrm{2}{arctan}\left(\sqrt{\frac{\mathrm{1}−{x}}{{x}}}\right) \\ $$$${f}'\left({x}\right)=? \\ $$
Commented by abdo mathsup 649 cc last updated on 13/Jul/18
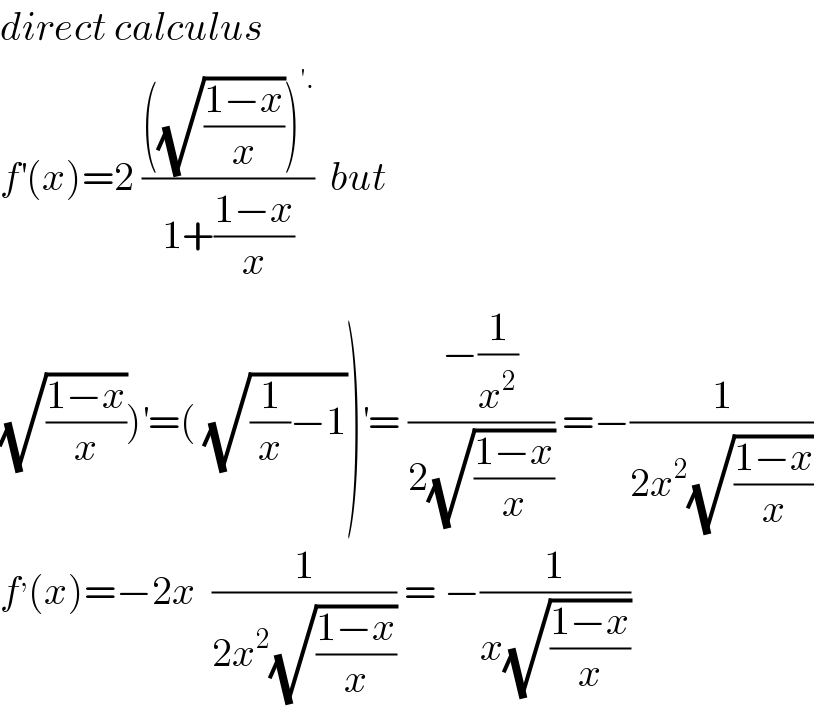
direct calculus f^′ (x)=2 ((((√((1−x)/x)))^(′.) )/(1+((1−x)/x))) but (√((1−x)/x)))^′ =( (√((1/x)−1)))^′ = ((−(1/x^2 ))/(2(√((1−x)/x)))) =−(1/(2x^2 (√((1−x)/x)))) f^, (x)=−2x (1/(2x^2 (√((1−x)/x)))) = −(1/(x(√((1−x)/x))))
$${direct}\:{calculus} \\ $$$${f}^{'} \left({x}\right)=\mathrm{2}\:\frac{\left(\sqrt{\frac{\mathrm{1}−{x}}{{x}}}\right)^{'.} }{\mathrm{1}+\frac{\mathrm{1}−{x}}{{x}}}\:\:{but} \\ $$$$\left.\sqrt{\frac{\mathrm{1}−{x}}{{x}}}\right)^{'} =\left(\:\sqrt{\frac{\mathrm{1}}{{x}}−\mathrm{1}}\right)^{'} =\:\frac{−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\mathrm{2}\sqrt{\frac{\mathrm{1}−{x}}{{x}}}}\:=−\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} \sqrt{\frac{\mathrm{1}−{x}}{{x}}}} \\ $$$${f}^{,} \left({x}\right)=−\mathrm{2}{x}\:\:\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} \sqrt{\frac{\mathrm{1}−{x}}{{x}}}}\:=\:−\frac{\mathrm{1}}{{x}\sqrt{\frac{\mathrm{1}−{x}}{{x}}}} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 13/Jul/18
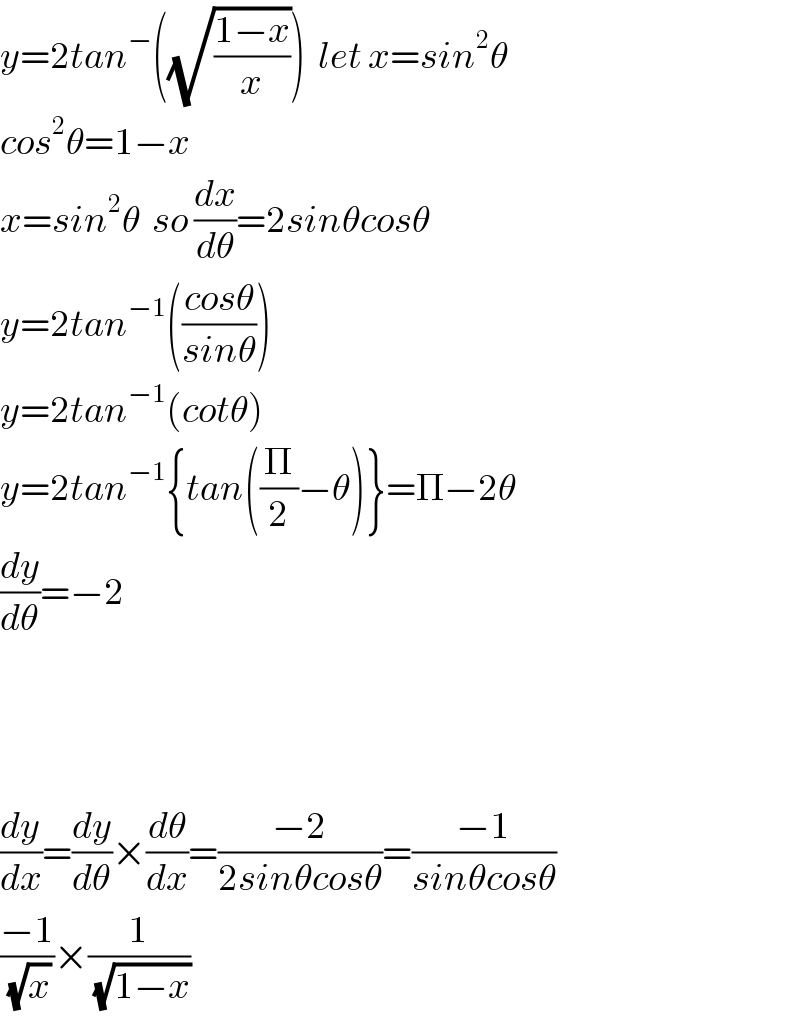
y=2tan^− ((√((1−x)/x))) let x=sin^2 θ cos^2 θ=1−x x=sin^2 θ so (dx/dθ)=2sinθcosθ y=2tan^(−1) (((cosθ)/(sinθ))) y=2tan^(−1) (cotθ) y=2tan^(−1) {tan((Π/2)−θ)}=Π−2θ (dy/dθ)=−2 (dy/dx)=(dy/dθ)×(dθ/dx)=((−2)/(2sinθcosθ))=((−1)/(sinθcosθ)) ((−1)/( (√x)))×(1/( (√(1−x))))
$${y}=\mathrm{2}{tan}^{−} \left(\sqrt{\frac{\mathrm{1}−{x}}{{x}}}\right)\:\:{let}\:{x}={sin}^{\mathrm{2}} \theta \\ $$$${cos}^{\mathrm{2}} \theta=\mathrm{1}−{x} \\ $$$${x}={sin}^{\mathrm{2}} \theta\:\:{so}\:\frac{{dx}}{{d}\theta}=\mathrm{2}{sin}\theta{cos}\theta \\ $$$${y}=\mathrm{2}{tan}^{−\mathrm{1}} \left(\frac{{cos}\theta}{{sin}\theta}\right) \\ $$$${y}=\mathrm{2}{tan}^{−\mathrm{1}} \left({cot}\theta\right) \\ $$$${y}=\mathrm{2}{tan}^{−\mathrm{1}} \left\{{tan}\left(\frac{\Pi}{\mathrm{2}}−\theta\right)\right\}=\Pi−\mathrm{2}\theta \\ $$$$\frac{{dy}}{{d}\theta}=−\mathrm{2} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$\frac{{dy}}{{dx}}=\frac{{dy}}{{d}\theta}×\frac{{d}\theta}{{dx}}=\frac{−\mathrm{2}}{\mathrm{2}{sin}\theta{cos}\theta}=\frac{−\mathrm{1}}{{sin}\theta{cos}\theta} \\ $$$$\frac{−\mathrm{1}}{\:\sqrt{{x}}}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}}} \\ $$
Answered by ajfour last updated on 13/Jul/18
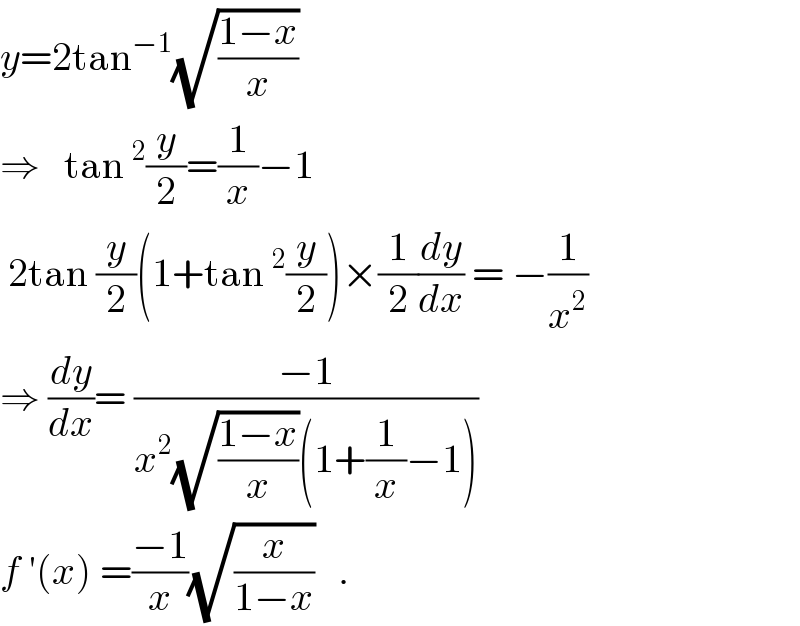
y=2tan^(−1) (√((1−x)/x)) ⇒ tan^2 (y/2)=(1/x)−1 2tan (y/2)(1+tan^2 (y/2))×(1/2)(dy/dx) = −(1/x^2 ) ⇒ (dy/dx)= ((−1)/(x^2 (√((1−x)/x))(1+(1/x)−1))) f ′(x) =((−1)/x)(√(x/(1−x))) .
$${y}=\mathrm{2tan}^{−\mathrm{1}} \sqrt{\frac{\mathrm{1}−{x}}{{x}}}\: \\ $$$$\Rightarrow\:\:\:\mathrm{tan}\:^{\mathrm{2}} \frac{{y}}{\mathrm{2}}=\frac{\mathrm{1}}{{x}}−\mathrm{1} \\ $$$$\:\mathrm{2tan}\:\frac{{y}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \frac{{y}}{\mathrm{2}}\right)×\frac{\mathrm{1}}{\mathrm{2}}\frac{{dy}}{{dx}}\:=\:−\frac{\mathrm{1}}{{x}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\frac{{dy}}{{dx}}=\:\frac{−\mathrm{1}}{{x}^{\mathrm{2}} \sqrt{\frac{\mathrm{1}−{x}}{{x}}}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}−\mathrm{1}\right)} \\ $$$${f}\:'\left({x}\right)\:=\frac{−\mathrm{1}}{{x}}\sqrt{\frac{{x}}{\mathrm{1}−{x}}}\:\:\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *