Menu Close

f-x-2x-3-x-2-2x-1-f-1-x-

Tinku Tara 0 Comments
Pin




Question Number 47778 by gunawan last updated on 14/Nov/18
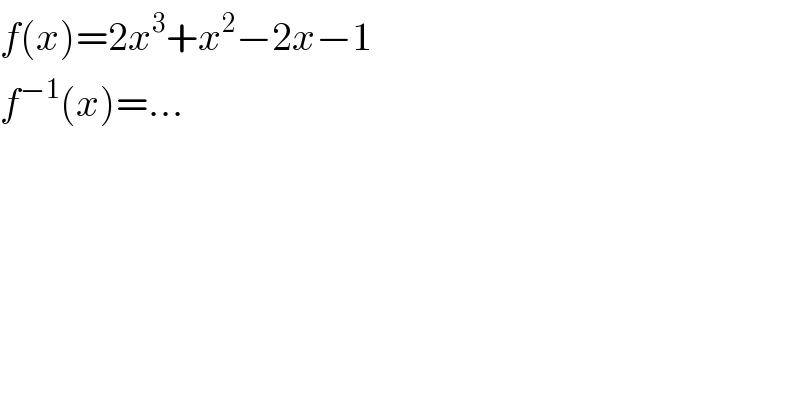
f(x)=2x^3 +x^2 −2x−1 f^(−1) (x)=...
$${f}\left({x}\right)=\mathrm{2}{x}^{\mathrm{3}} +{x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{1} \\ $$$${f}^{−\mathrm{1}} \left({x}\right)=… \\ $$
Answered by MJS last updated on 15/Nov/18
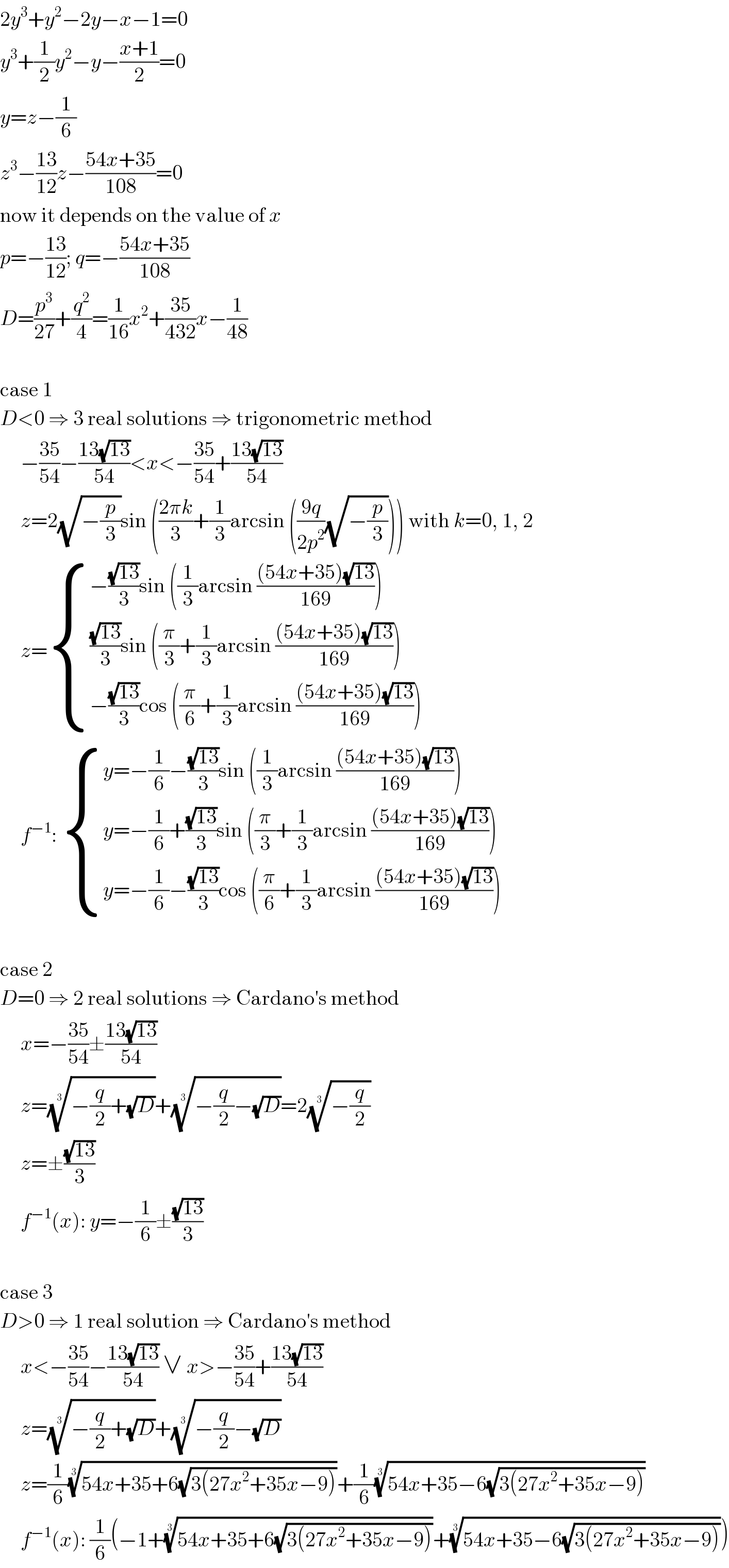
2y^3 +y^2 −2y−x−1=0 y^3 +(1/2)y^2 −y−((x+1)/2)=0 y=z−(1/6) z^3 −((13)/(12))z−((54x+35)/(108))=0 now it depends on the value of x p=−((13)/(12)); q=−((54x+35)/(108)) D=(p^3 /(27))+(q^2 /4)=(1/(16))x^2 +((35)/(432))x−(1/(48)) case 1 D<0 ⇒ 3 real solutions ⇒ trigonometric method −((35)/(54))−((13(√(13)))/(54))<x<−((35)/(54))+((13(√(13)))/(54)) z=2(√(−(p/3)))sin (((2πk)/3)+(1/3)arcsin (((9q)/(2p^2 ))(√(−(p/3))))) with k=0, 1, 2 z= { ((−((√(13))/3)sin ((1/3)arcsin (((54x+35)(√(13)))/(169))))),((((√(13))/3)sin ((π/3)+(1/3)arcsin (((54x+35)(√(13)))/(169))))),((−((√(13))/3)cos ((π/6)+(1/3)arcsin (((54x+35)(√(13)))/(169))))) :} f^(−1) : { ((y=−(1/6)−((√(13))/3)sin ((1/3)arcsin (((54x+35)(√(13)))/(169))))),((y=−(1/6)+((√(13))/3)sin ((π/3)+(1/3)arcsin (((54x+35)(√(13)))/(169))))),((y=−(1/6)−((√(13))/3)cos ((π/6)+(1/3)arcsin (((54x+35)(√(13)))/(169))))) :} case 2 D=0 ⇒ 2 real solutions ⇒ Cardano′s method x=−((35)/(54))±((13(√(13)))/(54)) z=((−(q/2)+(√D)))^(1/3) +((−(q/2)−(√D)))^(1/3) =2((−(q/2)))^(1/3) z=±((√(13))/3) f^(−1) (x): y=−(1/6)±((√(13))/3) case 3 D>0 ⇒ 1 real solution ⇒ Cardano′s method x<−((35)/(54))−((13(√(13)))/(54)) ∨ x>−((35)/(54))+((13(√(13)))/(54)) z=((−(q/2)+(√D)))^(1/3) +((−(q/2)−(√D)))^(1/3) z=(1/6)((54x+35+6(√(3(27x^2 +35x−9)))))^(1/3) +(1/6)((54x+35−6(√(3(27x^2 +35x−9)))))^(1/3) f^(−1) (x): (1/6)(−1+((54x+35+6(√(3(27x^2 +35x−9)))))^(1/3) +((54x+35−6(√(3(27x^2 +35x−9)))))^(1/3) )
$$\mathrm{2}{y}^{\mathrm{3}} +{y}^{\mathrm{2}} −\mathrm{2}{y}−{x}−\mathrm{1}=\mathrm{0} \\ $$$${y}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{2}}{y}^{\mathrm{2}} −{y}−\frac{{x}+\mathrm{1}}{\mathrm{2}}=\mathrm{0} \\ $$$${y}={z}−\frac{\mathrm{1}}{\mathrm{6}} \\ $$$${z}^{\mathrm{3}} −\frac{\mathrm{13}}{\mathrm{12}}{z}−\frac{\mathrm{54}{x}+\mathrm{35}}{\mathrm{108}}=\mathrm{0} \\ $$$$\mathrm{now}\:\mathrm{it}\:\mathrm{depends}\:\mathrm{on}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{x} \\ $$$${p}=−\frac{\mathrm{13}}{\mathrm{12}};\:{q}=−\frac{\mathrm{54}{x}+\mathrm{35}}{\mathrm{108}} \\ $$$${D}=\frac{{p}^{\mathrm{3}} }{\mathrm{27}}+\frac{{q}^{\mathrm{2}} }{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{16}}{x}^{\mathrm{2}} +\frac{\mathrm{35}}{\mathrm{432}}{x}−\frac{\mathrm{1}}{\mathrm{48}} \\ $$$$ \\ $$$$\mathrm{case}\:\mathrm{1} \\ $$$${D}<\mathrm{0}\:\Rightarrow\:\mathrm{3}\:\mathrm{real}\:\mathrm{solutions}\:\Rightarrow\:\mathrm{trigonometric}\:\mathrm{method} \\ $$$$\:\:\:\:\:−\frac{\mathrm{35}}{\mathrm{54}}−\frac{\mathrm{13}\sqrt{\mathrm{13}}}{\mathrm{54}}<{x}<−\frac{\mathrm{35}}{\mathrm{54}}+\frac{\mathrm{13}\sqrt{\mathrm{13}}}{\mathrm{54}} \\ $$$$\:\:\:\:\:{z}=\mathrm{2}\sqrt{−\frac{{p}}{\mathrm{3}}}\mathrm{sin}\:\left(\frac{\mathrm{2}\pi{k}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\left(\frac{\mathrm{9}{q}}{\mathrm{2}{p}^{\mathrm{2}} }\sqrt{−\frac{{p}}{\mathrm{3}}}\right)\right)\:\mathrm{with}\:{k}=\mathrm{0},\:\mathrm{1},\:\mathrm{2} \\ $$$$\:\:\:\:\:{z}=\begin{cases}{−\frac{\sqrt{\mathrm{13}}}{\mathrm{3}}\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\left(\mathrm{54}{x}+\mathrm{35}\right)\sqrt{\mathrm{13}}}{\mathrm{169}}\right)}\\{\frac{\sqrt{\mathrm{13}}}{\mathrm{3}}\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\left(\mathrm{54}{x}+\mathrm{35}\right)\sqrt{\mathrm{13}}}{\mathrm{169}}\right)}\\{−\frac{\sqrt{\mathrm{13}}}{\mathrm{3}}\mathrm{cos}\:\left(\frac{\pi}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\left(\mathrm{54}{x}+\mathrm{35}\right)\sqrt{\mathrm{13}}}{\mathrm{169}}\right)}\end{cases} \\ $$$$\:\:\:\:\:{f}^{−\mathrm{1}} :\:\begin{cases}{{y}=−\frac{\mathrm{1}}{\mathrm{6}}−\frac{\sqrt{\mathrm{13}}}{\mathrm{3}}\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\left(\mathrm{54}{x}+\mathrm{35}\right)\sqrt{\mathrm{13}}}{\mathrm{169}}\right)}\\{{y}=−\frac{\mathrm{1}}{\mathrm{6}}+\frac{\sqrt{\mathrm{13}}}{\mathrm{3}}\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\left(\mathrm{54}{x}+\mathrm{35}\right)\sqrt{\mathrm{13}}}{\mathrm{169}}\right)}\\{{y}=−\frac{\mathrm{1}}{\mathrm{6}}−\frac{\sqrt{\mathrm{13}}}{\mathrm{3}}\mathrm{cos}\:\left(\frac{\pi}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\left(\mathrm{54}{x}+\mathrm{35}\right)\sqrt{\mathrm{13}}}{\mathrm{169}}\right)}\end{cases} \\ $$$$ \\ $$$$\mathrm{case}\:\mathrm{2} \\ $$$${D}=\mathrm{0}\:\Rightarrow\:\mathrm{2}\:\mathrm{real}\:\mathrm{solutions}\:\Rightarrow\:\mathrm{Cardano}'\mathrm{s}\:\mathrm{method} \\ $$$$\:\:\:\:\:{x}=−\frac{\mathrm{35}}{\mathrm{54}}\pm\frac{\mathrm{13}\sqrt{\mathrm{13}}}{\mathrm{54}} \\ $$$$\:\:\:\:\:{z}=\sqrt[{\mathrm{3}}]{−\frac{{q}}{\mathrm{2}}+\sqrt{{D}}}+\sqrt[{\mathrm{3}}]{−\frac{{q}}{\mathrm{2}}−\sqrt{{D}}}=\mathrm{2}\sqrt[{\mathrm{3}}]{−\frac{{q}}{\mathrm{2}}} \\ $$$$\:\:\:\:\:{z}=\pm\frac{\sqrt{\mathrm{13}}}{\mathrm{3}} \\ $$$$\:\:\:\:\:{f}^{−\mathrm{1}} \left({x}\right):\:{y}=−\frac{\mathrm{1}}{\mathrm{6}}\pm\frac{\sqrt{\mathrm{13}}}{\mathrm{3}} \\ $$$$ \\ $$$$\mathrm{case}\:\mathrm{3} \\ $$$${D}>\mathrm{0}\:\Rightarrow\:\mathrm{1}\:\mathrm{real}\:\mathrm{solution}\:\Rightarrow\:\mathrm{Cardano}'\mathrm{s}\:\mathrm{method} \\ $$$$\:\:\:\:\:{x}<−\frac{\mathrm{35}}{\mathrm{54}}−\frac{\mathrm{13}\sqrt{\mathrm{13}}}{\mathrm{54}}\:\vee\:{x}>−\frac{\mathrm{35}}{\mathrm{54}}+\frac{\mathrm{13}\sqrt{\mathrm{13}}}{\mathrm{54}} \\ $$$$\:\:\:\:\:{z}=\sqrt[{\mathrm{3}}]{−\frac{{q}}{\mathrm{2}}+\sqrt{{D}}}+\sqrt[{\mathrm{3}}]{−\frac{{q}}{\mathrm{2}}−\sqrt{{D}}} \\ $$$$\:\:\:\:\:{z}=\frac{\mathrm{1}}{\mathrm{6}}\sqrt[{\mathrm{3}}]{\mathrm{54}{x}+\mathrm{35}+\mathrm{6}\sqrt{\mathrm{3}\left(\mathrm{27}{x}^{\mathrm{2}} +\mathrm{35}{x}−\mathrm{9}\right)}}+\frac{\mathrm{1}}{\mathrm{6}}\sqrt[{\mathrm{3}}]{\mathrm{54}{x}+\mathrm{35}−\mathrm{6}\sqrt{\mathrm{3}\left(\mathrm{27}{x}^{\mathrm{2}} +\mathrm{35}{x}−\mathrm{9}\right)}} \\ $$$$\:\:\:\:\:{f}^{−\mathrm{1}} \left({x}\right):\:\frac{\mathrm{1}}{\mathrm{6}}\left(−\mathrm{1}+\sqrt[{\mathrm{3}}]{\mathrm{54}{x}+\mathrm{35}+\mathrm{6}\sqrt{\mathrm{3}\left(\mathrm{27}{x}^{\mathrm{2}} +\mathrm{35}{x}−\mathrm{9}\right)}}+\sqrt[{\mathrm{3}}]{\mathrm{54}{x}+\mathrm{35}−\mathrm{6}\sqrt{\mathrm{3}\left(\mathrm{27}{x}^{\mathrm{2}} +\mathrm{35}{x}−\mathrm{9}\right)}}\right) \\ $$
Commented by gunawan last updated on 21/Nov/18
thanks
$$\mathrm{thanks} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *