Question Number 165153 by mathlove last updated on 26/Jan/22

$${f}\left({x}\right)=\mathrm{3}{e}^{\mathrm{2}{x}} \\ $$$${f}^{−\mathrm{1}} \left({x}\right)=? \\ $$
Answered by mahdipoor last updated on 26/Jan/22
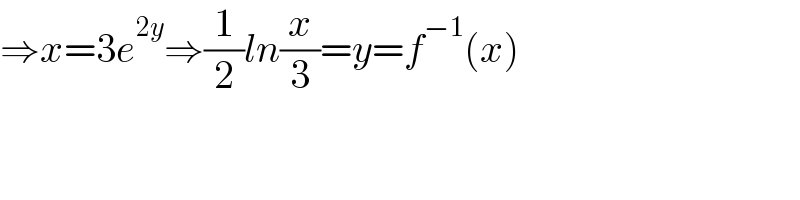
$$\Rightarrow{x}=\mathrm{3}{e}^{\mathrm{2}{y}} \Rightarrow\frac{\mathrm{1}}{\mathrm{2}}{ln}\frac{{x}}{\mathrm{3}}={y}={f}^{−\mathrm{1}} \left({x}\right) \\ $$
Answered by MathsFan last updated on 27/Jan/22

$${let}\:\:{y}=\mathrm{3}{e}^{\mathrm{2}{x}} \\ $$$$\:{x}=\mathrm{3}{e}^{\mathrm{2}{y}} \:\rightarrow\:\:{logx}=\mathrm{2}{ylog}\mathrm{3}{e} \\ $$$$\rightarrow\:\mathrm{2}{y}={log}_{\mathrm{3}{e}} {x}\:\rightarrow\:{y}=\frac{{log}_{\mathrm{3}{e}} {x}}{\mathrm{2}}\: \\ $$$${f}^{−\mathrm{1}} \left({x}\right)=\frac{{log}_{\mathrm{3}{e}} {x}}{\mathrm{2}} \\ $$$$ \\ $$
Answered by alephzero last updated on 28/Jan/22

$${f}\left({x}\right)\:=\:\mathrm{3}{e}^{\mathrm{2}{x}} \\ $$$${f}^{−\mathrm{1}} \left({x}\right)\:=\:? \\ $$$${x}\:=\:\mathrm{3}{e}^{\mathrm{2}{y}} \\ $$$$\Rightarrow\:\frac{{x}}{\mathrm{3}}\:=\:{e}^{\mathrm{2}{y}} \\ $$$$\Rightarrow\:\mathrm{ln}\:\frac{{x}}{\mathrm{3}}\:=\:\mathrm{2}{y} \\ $$$$\Rightarrow\:\frac{\mathrm{ln}\:\frac{{x}}{\mathrm{3}}}{\mathrm{2}}\:=\:\frac{\mathrm{ln}\:{x}\:−\:\mathrm{ln}\:\mathrm{3}}{\mathrm{2}}\:=\:{y} \\ $$$$\Rightarrow\:{f}^{−\mathrm{1}} \left({x}\right)\:=\:\frac{\mathrm{ln}\:{x}\:−\:\mathrm{ln}\:\mathrm{3}}{\mathrm{2}} \\ $$
