Question Number 185574 by mnjuly1970 last updated on 23/Jan/23
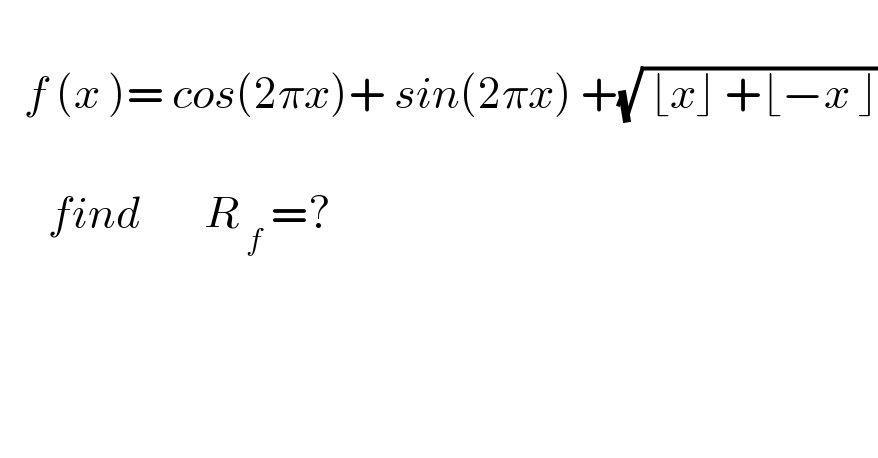
$$ \\ $$$$\:\:\:{f}\:\left({x}\:\right)=\:{cos}\left(\mathrm{2}\pi{x}\right)+\:{sin}\left(\mathrm{2}\pi{x}\right)\:+\sqrt{\:\lfloor{x}\rfloor\:+\lfloor−{x}\:\rfloor} \\ $$$$\:\:\: \\ $$$$\:\:\:\:\:\:{find}\:\:\:\:\:\:\:\:{R}_{\:{f}} \:=? \\ $$
Commented by mahdipoor last updated on 23/Jan/23
![(√([x]+[−x]))= { ((0 x∈Z)),(((√(−1))=i x∉Z)) :} ⇒D_f =Z⇒f(x)=cos(2πk)+sin(2πk)+0=1](https://www.tinkutara.com/question/Q185589.png)
$$\sqrt{\left[{x}\right]+\left[−{x}\right]}=\begin{cases}{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}\in{Z}}\\{\sqrt{−\mathrm{1}}={i}\:\:\:\:\:{x}\notin{Z}}\end{cases}\:\: \\ $$$$\Rightarrow{D}_{{f}} ={Z}\Rightarrow{f}\left({x}\right)={cos}\left(\mathrm{2}\pi{k}\right)+{sin}\left(\mathrm{2}\pi{k}\right)+\mathrm{0}=\mathrm{1} \\ $$
