Question Number 87352 by jagoll last updated on 04/Apr/20
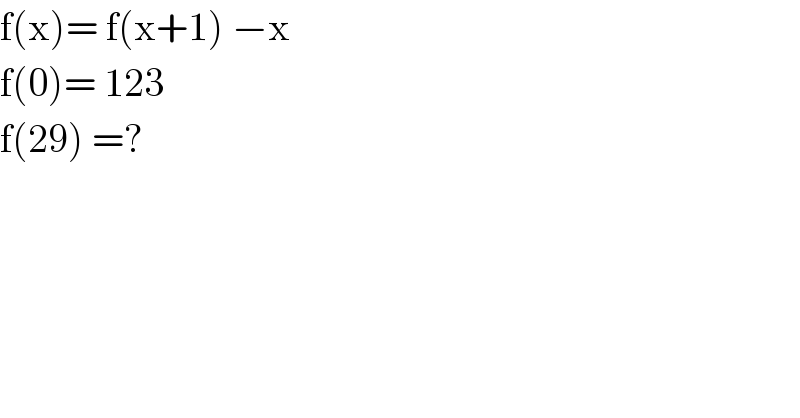
$$\mathrm{f}\left(\mathrm{x}\right)=\:\mathrm{f}\left(\mathrm{x}+\mathrm{1}\right)\:−\mathrm{x} \\ $$$$\mathrm{f}\left(\mathrm{0}\right)=\:\mathrm{123} \\ $$$$\mathrm{f}\left(\mathrm{29}\right)\:=? \\ $$
Commented by jagoll last updated on 04/Apr/20
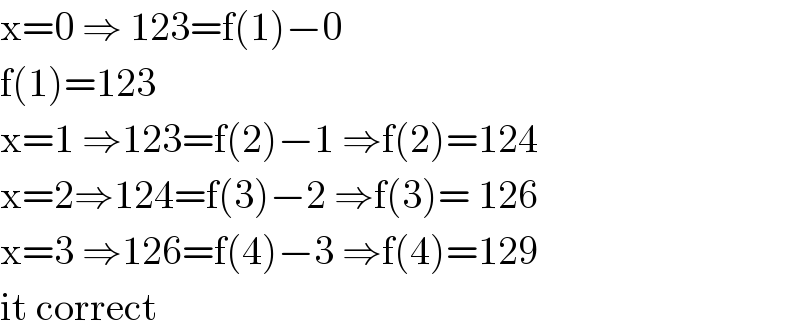
$$\mathrm{x}=\mathrm{0}\:\Rightarrow\:\mathrm{123}=\mathrm{f}\left(\mathrm{1}\right)−\mathrm{0} \\ $$$$\mathrm{f}\left(\mathrm{1}\right)=\mathrm{123} \\ $$$$\mathrm{x}=\mathrm{1}\:\Rightarrow\mathrm{123}=\mathrm{f}\left(\mathrm{2}\right)−\mathrm{1}\:\Rightarrow\mathrm{f}\left(\mathrm{2}\right)=\mathrm{124} \\ $$$$\mathrm{x}=\mathrm{2}\Rightarrow\mathrm{124}=\mathrm{f}\left(\mathrm{3}\right)−\mathrm{2}\:\Rightarrow\mathrm{f}\left(\mathrm{3}\right)=\:\mathrm{126} \\ $$$$\mathrm{x}=\mathrm{3}\:\Rightarrow\mathrm{126}=\mathrm{f}\left(\mathrm{4}\right)−\mathrm{3}\:\Rightarrow\mathrm{f}\left(\mathrm{4}\right)=\mathrm{129} \\ $$$$\mathrm{it}\:\mathrm{correct} \\ $$
Commented by jagoll last updated on 04/Apr/20
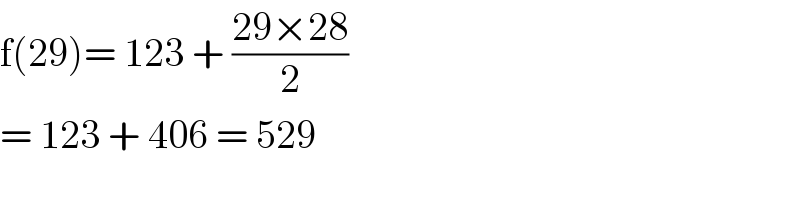
$$\mathrm{f}\left(\mathrm{29}\right)=\:\mathrm{123}\:+\:\frac{\mathrm{29}×\mathrm{28}}{\mathrm{2}} \\ $$$$=\:\mathrm{123}\:+\:\mathrm{406}\:=\:\mathrm{529} \\ $$
Commented by jagoll last updated on 04/Apr/20
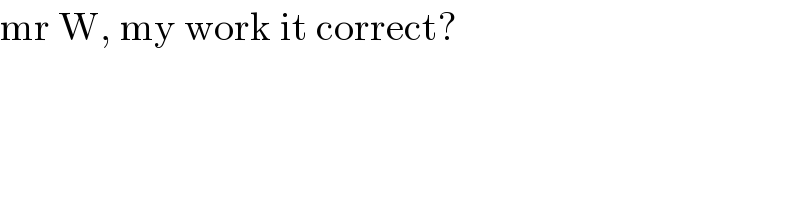
$$\mathrm{mr}\:\mathrm{W},\:\mathrm{my}\:\mathrm{work}\:\mathrm{it}\:\mathrm{correct}? \\ $$
Commented by mr W last updated on 04/Apr/20

$${yes} \\ $$
Commented by john santu last updated on 04/Apr/20
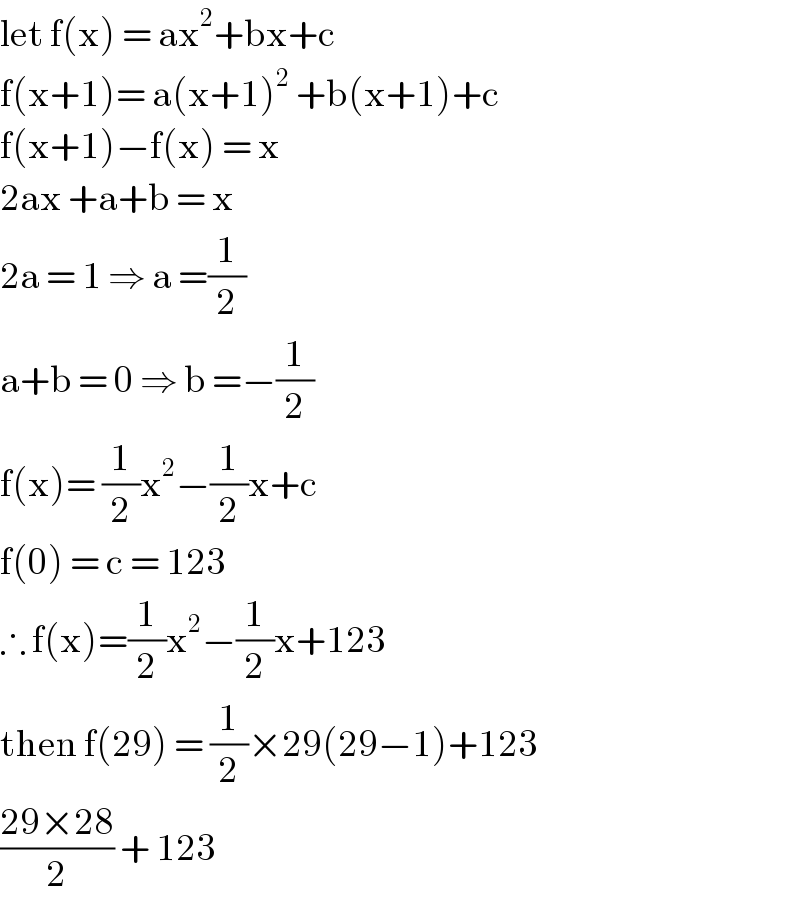
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\mathrm{ax}^{\mathrm{2}} +\mathrm{bx}+\mathrm{c} \\ $$$$\mathrm{f}\left(\mathrm{x}+\mathrm{1}\right)=\:\mathrm{a}\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{b}\left(\mathrm{x}+\mathrm{1}\right)+\mathrm{c} \\ $$$$\mathrm{f}\left(\mathrm{x}+\mathrm{1}\right)−\mathrm{f}\left(\mathrm{x}\right)\:=\:\mathrm{x} \\ $$$$\mathrm{2ax}\:+\mathrm{a}+\mathrm{b}\:=\:\mathrm{x}\: \\ $$$$\mathrm{2a}\:=\:\mathrm{1}\:\Rightarrow\:\mathrm{a}\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{a}+\mathrm{b}\:=\:\mathrm{0}\:\Rightarrow\:\mathrm{b}\:=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}+\mathrm{c} \\ $$$$\mathrm{f}\left(\mathrm{0}\right)\:=\:\mathrm{c}\:=\:\mathrm{123} \\ $$$$\therefore\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}+\mathrm{123} \\ $$$$\mathrm{then}\:\mathrm{f}\left(\mathrm{29}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{29}\left(\mathrm{29}−\mathrm{1}\right)+\mathrm{123} \\ $$$$\frac{\mathrm{29}×\mathrm{28}}{\mathrm{2}}\:+\:\mathrm{123}\: \\ $$
Commented by jagoll last updated on 04/Apr/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 04/Apr/20
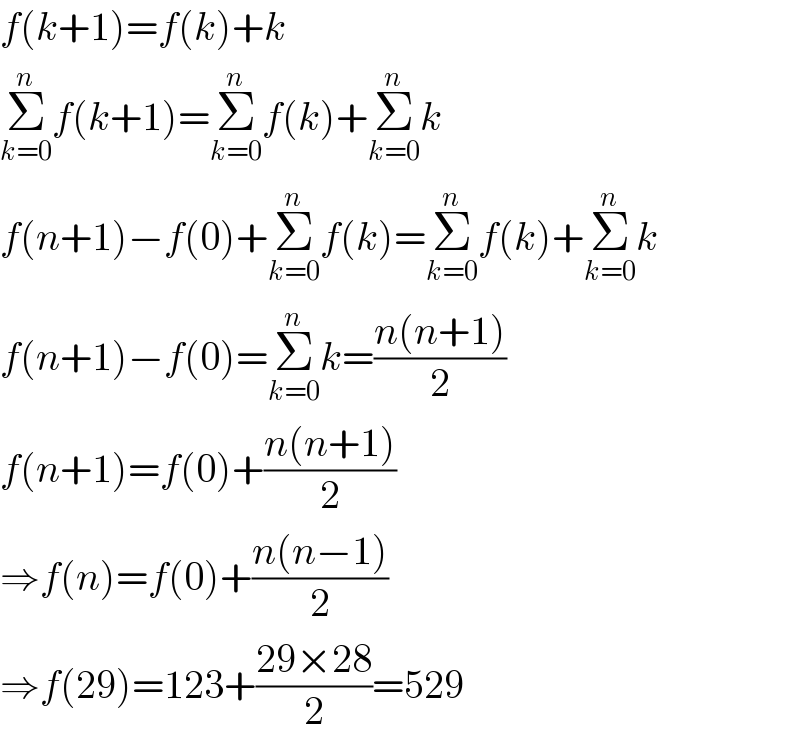
$${f}\left({k}+\mathrm{1}\right)={f}\left({k}\right)+{k} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{f}\left({k}+\mathrm{1}\right)=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{f}\left({k}\right)+\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{k} \\ $$$${f}\left({n}+\mathrm{1}\right)−{f}\left(\mathrm{0}\right)+\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{f}\left({k}\right)=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{f}\left({k}\right)+\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{k} \\ $$$${f}\left({n}+\mathrm{1}\right)−{f}\left(\mathrm{0}\right)=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{k}=\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$${f}\left({n}+\mathrm{1}\right)={f}\left(\mathrm{0}\right)+\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\Rightarrow{f}\left({n}\right)={f}\left(\mathrm{0}\right)+\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\Rightarrow{f}\left(\mathrm{29}\right)=\mathrm{123}+\frac{\mathrm{29}×\mathrm{28}}{\mathrm{2}}=\mathrm{529} \\ $$
Commented by jagoll last updated on 04/Apr/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
