Question Number 176332 by Linton last updated on 16/Sep/22
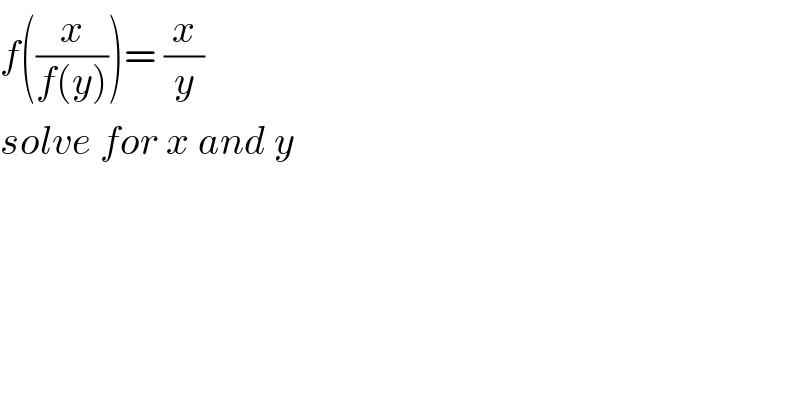
$${f}\left(\frac{{x}}{{f}\left({y}\right)}\right)=\:\frac{{x}}{{y}} \\ $$$${solve}\:{for}\:{x}\:{and}\:{y} \\ $$
Commented by mr W last updated on 16/Sep/22
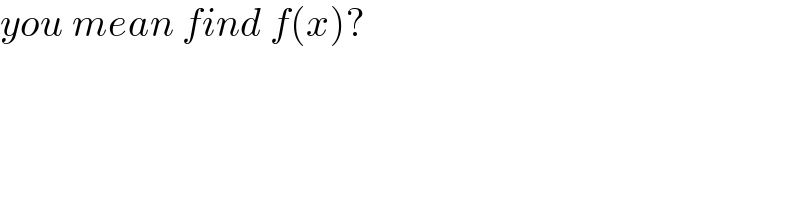
$${you}\:{mean}\:{find}\:{f}\left({x}\right)? \\ $$
Answered by mr W last updated on 16/Sep/22
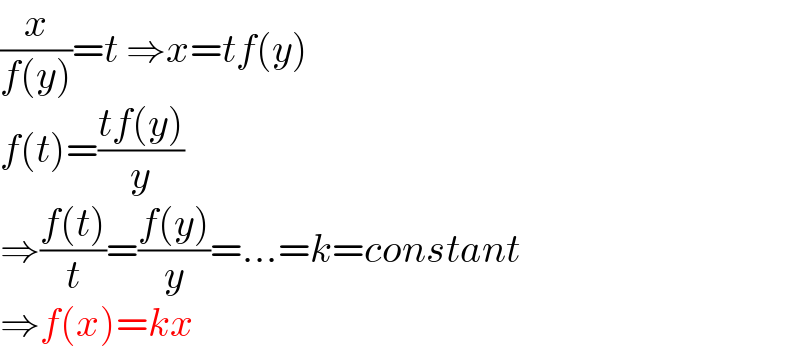
$$\frac{{x}}{{f}\left({y}\right)}={t}\:\Rightarrow{x}={tf}\left({y}\right) \\ $$$${f}\left({t}\right)=\frac{{tf}\left({y}\right)}{{y}} \\ $$$$\Rightarrow\frac{{f}\left({t}\right)}{{t}}=\frac{{f}\left({y}\right)}{{y}}=…={k}={constant} \\ $$$$\Rightarrow{f}\left({x}\right)={kx} \\ $$
Commented by Linton last updated on 17/Sep/22

$${solve}\:{for}\:{x}\:{and}\:{y}\:? \\ $$
Commented by mr W last updated on 17/Sep/22
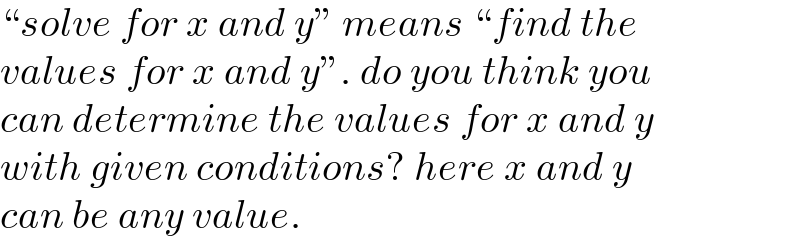
$$“{solve}\:{for}\:{x}\:{and}\:{y}''\:{means}\:“{find}\:{the} \\ $$$${values}\:{for}\:{x}\:{and}\:{y}''.\:{do}\:{you}\:{think}\:{you} \\ $$$${can}\:{determine}\:{the}\:{values}\:{for}\:{x}\:{and}\:{y} \\ $$$${with}\:{given}\:{conditions}?\:{here}\:{x}\:{and}\:{y} \\ $$$${can}\:{be}\:{any}\:{value}. \\ $$
