Menu Close

f-x-g-x-and-g-x-f-x-for-all-real-x-andf-5-2-f-5-then-f-2-10-g-2-10-is-a-2-b-4-c-8-d-none-

Tinku Tara 0 Comments
Pin




Question Number 40052 by LXZ last updated on 15/Jul/18
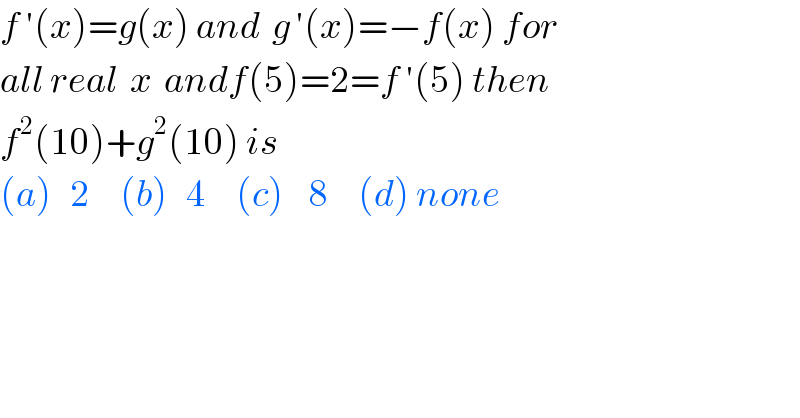
f ′(x)=g(x) and g ′(x)=−f(x) for all real x andf(5)=2=f ′(5) then f^2 (10)+g^2 (10) is (a) 2 (b) 4 (c) 8 (d) none
$${f}\:'\left({x}\right)={g}\left({x}\right)\:{and}\:\:{g}\:'\left({x}\right)=−{f}\left({x}\right)\:{for} \\ $$$${all}\:{real}\:\:{x}\:\:{andf}\left(\mathrm{5}\right)=\mathrm{2}={f}\:'\left(\mathrm{5}\right)\:{then} \\ $$$${f}^{\mathrm{2}} \left(\mathrm{10}\right)+{g}^{\mathrm{2}} \left(\mathrm{10}\right)\:{is} \\ $$$$\left({a}\right)\:\:\:\mathrm{2}\:\:\:\:\:\left({b}\right)\:\:\:\mathrm{4}\:\:\:\:\:\left({c}\right)\:\:\:\:\mathrm{8}\:\:\:\:\:\left({d}\right)\:{none} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 15/Jul/18
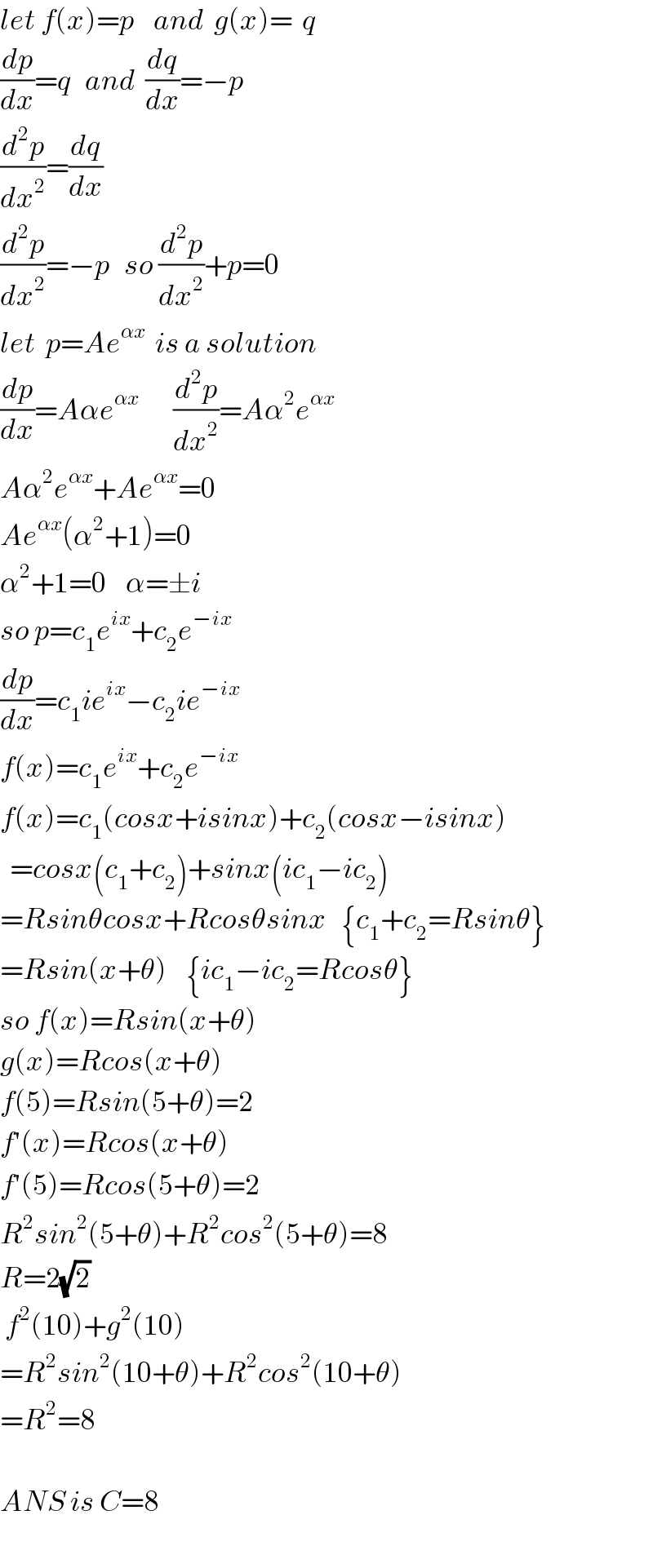
let f(x)=p and g(x)= q (dp/dx)=q and (dq/dx)=−p (d^2 p/dx^2 )=(dq/dx) (d^2 p/dx^2 )=−p so (d^2 p/dx^2 )+p=0 let p=Ae^(αx) is a solution (dp/dx)=Aαe^(αx) (d^2 p/dx^2 )=Aα^2 e^(αx) Aα^2 e^(αx) +Ae^(αx) =0 Ae^(αx) (α^2 +1)=0 α^2 +1=0 α=±i so p=c_1 e^(ix) +c_2 e^(−ix) (dp/dx)=c_1 ie^(ix) −c_2 ie^(−ix) f(x)=c_1 e^(ix) +c_2 e^(−ix) f(x)=c_1 (cosx+isinx)+c_2 (cosx−isinx) =cosx(c_1 +c_2 )+sinx(ic_1 −ic_2 ) =Rsinθcosx+Rcosθsinx {c_1 +c_2 =Rsinθ} =Rsin(x+θ) {ic_1 −ic_2 =Rcosθ} so f(x)=Rsin(x+θ) g(x)=Rcos(x+θ) f(5)=Rsin(5+θ)=2 f′(x)=Rcos(x+θ) f′(5)=Rcos(5+θ)=2 R^2 sin^2 (5+θ)+R^2 cos^2 (5+θ)=8 R=2(√2) f^2 (10)+g^2 (10) =R^2 sin^2 (10+θ)+R^2 cos^2 (10+θ) =R^2 =8 ANS is C=8
$${let}\:{f}\left({x}\right)={p}\:\:\:\:{and}\:\:{g}\left({x}\right)=\:\:{q} \\ $$$$\frac{{dp}}{{dx}}={q}\:\:\:{and}\:\:\frac{{dq}}{{dx}}=−{p} \\ $$$$\frac{{d}^{\mathrm{2}} {p}}{{dx}^{\mathrm{2}} }=\frac{{dq}}{{dx}} \\ $$$$\frac{{d}^{\mathrm{2}} {p}}{{dx}^{\mathrm{2}} }=−{p}\:\:\:{so}\:\frac{{d}^{\mathrm{2}} {p}}{{dx}^{\mathrm{2}} }+{p}=\mathrm{0} \\ $$$${let}\:\:{p}={Ae}^{\alpha{x}} \:\:{is}\:{a}\:{solution} \\ $$$$\frac{{dp}}{{dx}}={A}\alpha{e}^{\alpha{x}} \:\:\:\:\:\:\:\frac{{d}^{\mathrm{2}} {p}}{{dx}^{\mathrm{2}} }={A}\alpha^{\mathrm{2}} {e}^{\alpha{x}} \\ $$$${A}\alpha^{\mathrm{2}} {e}^{\alpha{x}} +{Ae}^{\alpha{x}} =\mathrm{0} \\ $$$${Ae}^{\alpha{x}} \left(\alpha^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{0} \\ $$$$\alpha^{\mathrm{2}} +\mathrm{1}=\mathrm{0}\:\:\:\:\alpha=\pm{i} \\ $$$${so}\:{p}={c}_{\mathrm{1}} {e}^{{ix}} +{c}_{\mathrm{2}} {e}^{−{ix}} \\ $$$$\frac{{dp}}{{dx}}={c}_{\mathrm{1}} {ie}^{{ix}} −{c}_{\mathrm{2}} {ie}^{−{ix}} \\ $$$${f}\left({x}\right)={c}_{\mathrm{1}} {e}^{{ix}} +{c}_{\mathrm{2}} {e}^{−{ix}} \\ $$$${f}\left({x}\right)={c}_{\mathrm{1}} \left({cosx}+{isinx}\right)+{c}_{\mathrm{2}} \left({cosx}−{isinx}\right) \\ $$$$\:\:={cosx}\left({c}_{\mathrm{1}} +{c}_{\mathrm{2}} \right)+{sinx}\left({ic}_{\mathrm{1}} −{ic}_{\mathrm{2}} \right) \\ $$$$={Rsin}\theta{cosx}+{Rcos}\theta{sinx}\:\:\:\left\{{c}_{\mathrm{1}} +{c}_{\mathrm{2}} ={Rsin}\theta\right\} \\ $$$$={Rsin}\left({x}+\theta\right)\:\:\:\:\left\{{ic}_{\mathrm{1}} −{ic}_{\mathrm{2}} ={Rcos}\theta\right\} \\ $$$${so}\:{f}\left({x}\right)={Rsin}\left({x}+\theta\right) \\ $$$${g}\left({x}\right)={Rcos}\left({x}+\theta\right) \\ $$$${f}\left(\mathrm{5}\right)={Rsin}\left(\mathrm{5}+\theta\right)=\mathrm{2} \\ $$$${f}'\left({x}\right)={Rcos}\left({x}+\theta\right) \\ $$$${f}'\left(\mathrm{5}\right)={Rcos}\left(\mathrm{5}+\theta\right)=\mathrm{2} \\ $$$${R}^{\mathrm{2}} {sin}^{\mathrm{2}} \left(\mathrm{5}+\theta\right)+{R}^{\mathrm{2}} {cos}^{\mathrm{2}} \left(\mathrm{5}+\theta\right)=\mathrm{8} \\ $$$${R}=\mathrm{2}\sqrt{\mathrm{2}}\: \\ $$$$\:{f}^{\mathrm{2}} \left(\mathrm{10}\right)+{g}^{\mathrm{2}} \left(\mathrm{10}\right) \\ $$$$={R}^{\mathrm{2}} {sin}^{\mathrm{2}} \left(\mathrm{10}+\theta\right)+{R}^{\mathrm{2}} {cos}^{\mathrm{2}} \left(\mathrm{10}+\theta\right) \\ $$$$={R}^{\mathrm{2}} =\mathrm{8} \\ $$$$ \\ $$$${ANS}\:{is}\:{C}=\mathrm{8} \\ $$
Commented by LXZ last updated on 15/Jul/18
thanks sir
$${thanks}\:{sir} \\ $$$$ \\ $$
Answered by ajfour last updated on 16/Jul/18
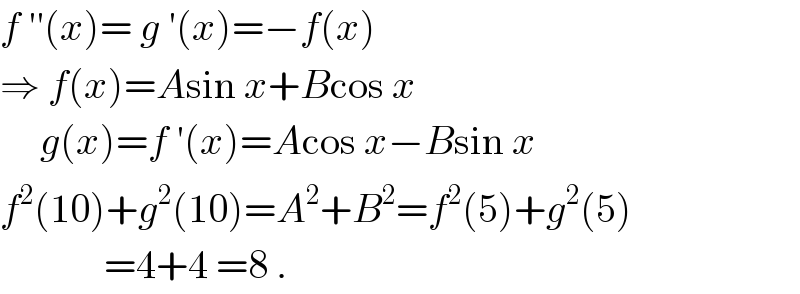
f ′′(x)= g ′(x)=−f(x) ⇒ f(x)=Asin x+Bcos x g(x)=f ′(x)=Acos x−Bsin x f^2 (10)+g^2 (10)=A^2 +B^2 =f^2 (5)+g^2 (5) =4+4 =8 .
$${f}\:''\left({x}\right)=\:{g}\:'\left({x}\right)=−{f}\left({x}\right) \\ $$$$\Rightarrow\:{f}\left({x}\right)={A}\mathrm{sin}\:{x}+{B}\mathrm{cos}\:{x} \\ $$$$\:\:\:\:\:{g}\left({x}\right)={f}\:'\left({x}\right)={A}\mathrm{cos}\:{x}−{B}\mathrm{sin}\:{x} \\ $$$${f}^{\mathrm{2}} \left(\mathrm{10}\right)+{g}^{\mathrm{2}} \left(\mathrm{10}\right)={A}^{\mathrm{2}} +{B}^{\mathrm{2}} ={f}^{\mathrm{2}} \left(\mathrm{5}\right)+{g}^{\mathrm{2}} \left(\mathrm{5}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{4}+\mathrm{4}\:=\mathrm{8}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *