Question Number 57754 by malwaan last updated on 11/Apr/19

$$\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)=\boldsymbol{{ln}}\left(\boldsymbol{{x}}\right) \\ $$$$\left(\boldsymbol{{f}}\circ\boldsymbol{{f}}\right)'=? \\ $$
Commented by maxmathsup by imad last updated on 11/Apr/19
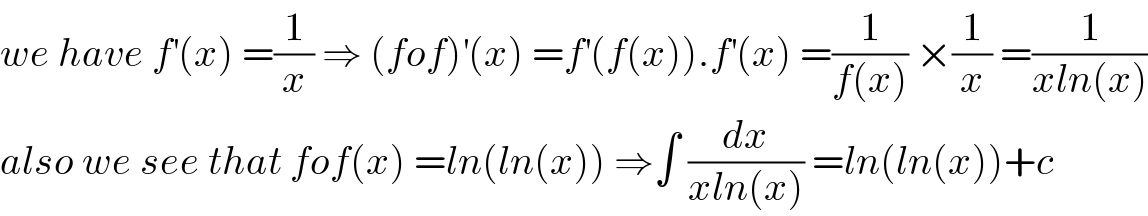
$${we}\:{have}\:{f}^{'} \left({x}\right)\:=\frac{\mathrm{1}}{{x}}\:\Rightarrow\:\left({fof}\right)^{'} \left({x}\right)\:={f}^{'} \left({f}\left({x}\right)\right).{f}^{'} \left({x}\right)\:=\frac{\mathrm{1}}{{f}\left({x}\right)}\:×\frac{\mathrm{1}}{{x}}\:=\frac{\mathrm{1}}{{xln}\left({x}\right)} \\ $$$${also}\:{we}\:{see}\:{that}\:{fof}\left({x}\right)\:={ln}\left({ln}\left({x}\right)\right)\:\Rightarrow\int\:\frac{{dx}}{{xln}\left({x}\right)}\:={ln}\left({ln}\left({x}\right)\right)+{c}\: \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 11/Apr/19
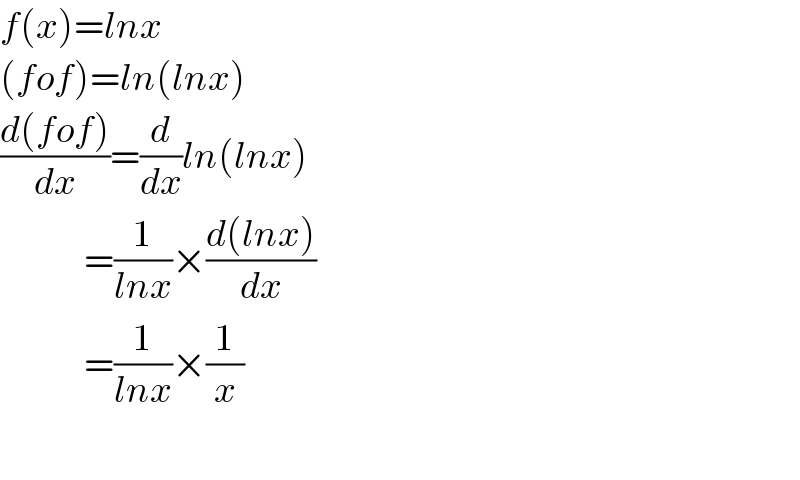
$${f}\left({x}\right)={lnx} \\ $$$$\left({fof}\right)={ln}\left({lnx}\right) \\ $$$$\frac{{d}\left({fof}\right)}{{dx}}=\frac{{d}}{{dx}}{ln}\left({lnx}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{{lnx}}×\frac{{d}\left({lnx}\right)}{{dx}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{{lnx}}×\frac{\mathrm{1}}{{x}} \\ $$$$ \\ $$
Commented by malwaan last updated on 11/Apr/19
$$\boldsymbol{{thank}}\:\boldsymbol{{you}}\:\boldsymbol{{sir}} \\ $$
Answered by MJS last updated on 11/Apr/19
![f○f=ln (ln x) =f(f(x)) (d/dx)v(u(x))=v′(u(x))×u′(x) (d/dx)[ln (ln x)]=(1/(ln x))×(1/x)=(1/(xln x))](https://www.tinkutara.com/question/Q57762.png)
$${f}\circ{f}=\mathrm{ln}\:\left(\mathrm{ln}\:{x}\right)\:={f}\left({f}\left({x}\right)\right) \\ $$$$\frac{{d}}{{dx}}{v}\left({u}\left({x}\right)\right)={v}'\left({u}\left({x}\right)\right)×{u}'\left({x}\right) \\ $$$$\frac{{d}}{{dx}}\left[\mathrm{ln}\:\left(\mathrm{ln}\:{x}\right)\right]=\frac{\mathrm{1}}{\mathrm{ln}\:{x}}×\frac{\mathrm{1}}{{x}}=\frac{\mathrm{1}}{{x}\mathrm{ln}\:{x}} \\ $$
Commented by malwaan last updated on 11/Apr/19
$$\boldsymbol{{thank}}\:\boldsymbol{{you}}\:\boldsymbol{{sir}} \\ $$
