Question Number 15181 by Joel577 last updated on 08/Jun/17
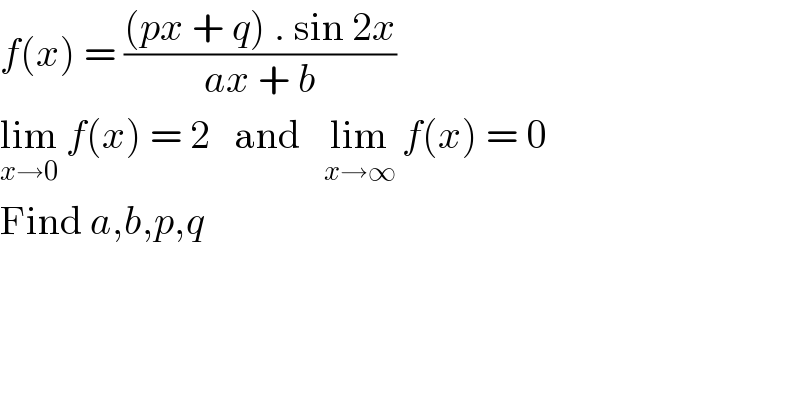
$${f}\left({x}\right)\:=\:\frac{\left({px}\:+\:{q}\right)\:.\:\mathrm{sin}\:\mathrm{2}{x}}{{ax}\:+\:{b}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{f}\left({x}\right)\:=\:\mathrm{2}\:\:\:\mathrm{and}\:\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{f}\left({x}\right)\:=\:\mathrm{0} \\ $$$$\mathrm{Find}\:{a},{b},{p},{q}\:\: \\ $$
Answered by ajfour last updated on 08/Jun/17
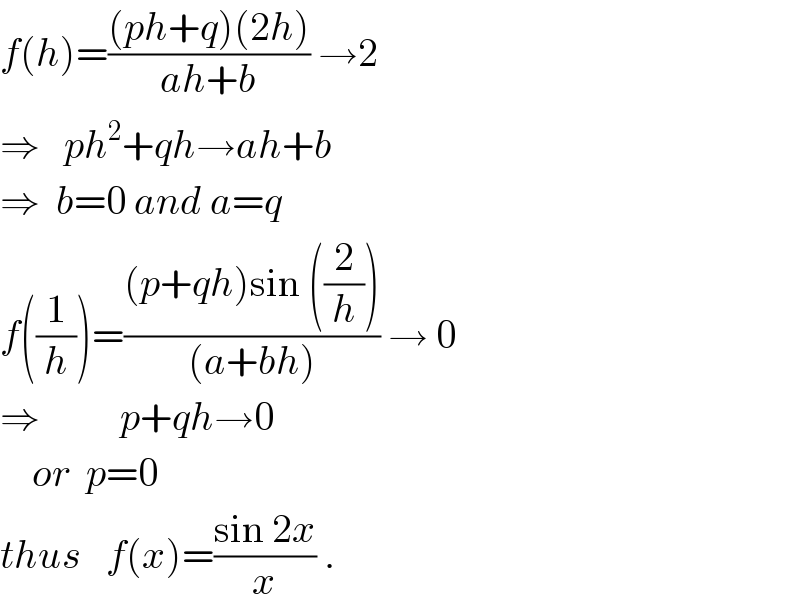
$${f}\left({h}\right)=\frac{\left({ph}+{q}\right)\left(\mathrm{2}{h}\right)}{{ah}+{b}}\:\rightarrow\mathrm{2} \\ $$$$\Rightarrow\:\:\:{ph}^{\mathrm{2}} +{qh}\rightarrow{ah}+{b} \\ $$$$\Rightarrow\:\:{b}=\mathrm{0}\:{and}\:{a}={q} \\ $$$${f}\left(\frac{\mathrm{1}}{{h}}\right)=\frac{\left({p}+{qh}\right)\mathrm{sin}\:\left(\frac{\mathrm{2}}{{h}}\right)}{\left({a}+{bh}\right)}\:\rightarrow\:\mathrm{0} \\ $$$$\Rightarrow\:\:\:\:\:\:\:\:\:\:{p}+{qh}\rightarrow\mathrm{0} \\ $$$$\:\:\:\:{or}\:\:{p}=\mathrm{0} \\ $$$${thus}\:\:\:{f}\left({x}\right)=\frac{\mathrm{sin}\:\mathrm{2}{x}}{{x}}\:. \\ $$
