Question Number 146899 by mathmax by abdo last updated on 16/Jul/21
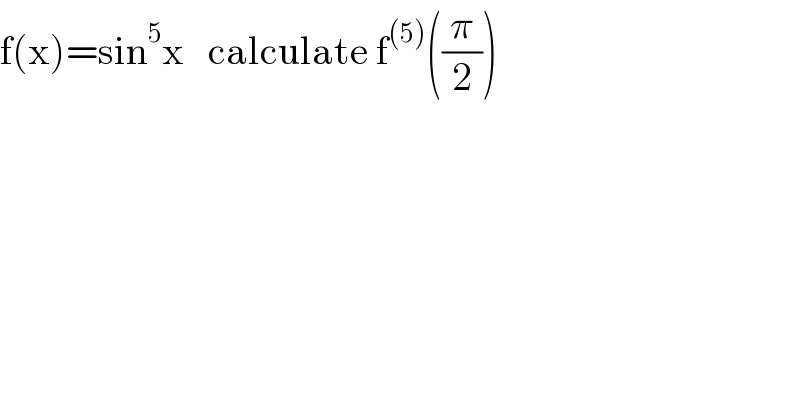
$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{sin}^{\mathrm{5}} \mathrm{x}\:\:\:\mathrm{calculate}\:\mathrm{f}^{\left(\mathrm{5}\right)} \left(\frac{\pi}{\mathrm{2}}\right) \\ $$
Answered by Olaf_Thorendsen last updated on 17/Jul/21

$${f}\left({x}\right)\:=\:\mathrm{sin}^{\mathrm{5}} {x} \\ $$$${f}\left({x}\right)\:=\:\left(\frac{{e}^{{ix}} −{e}^{{ix}} }{\mathrm{2}{i}}\right)^{\mathrm{5}} \\ $$$${f}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{16}×\mathrm{2}{i}}\left({e}^{\mathrm{5}{ix}} −\mathrm{5}{e}^{\mathrm{3}{ix}} +\mathrm{10}{e}^{{ix}} −\mathrm{10}{e}^{−{ix}} +\mathrm{5}{e}^{−\mathrm{3}{ix}} −{e}^{−\mathrm{5}{ix}} \right) \\ $$$${f}\left({x}\right)\:=\:\frac{\mathrm{sin5}{x}−\mathrm{5sin3}{x}+\mathrm{10sin}{x}}{\mathrm{16}} \\ $$$${f}^{\left(\mathrm{5}\right)} \left({x}\right)\:=\:\frac{\mathrm{5}^{\mathrm{5}} \mathrm{cos5}{x}−\mathrm{5}.\mathrm{3}^{\mathrm{5}} \mathrm{cos3}{x}+\mathrm{10cos}{x}}{\mathrm{16}} \\ $$$${f}^{\left(\mathrm{5}\right)} \left(\frac{\pi}{\mathrm{2}}\right)\:=\:\mathrm{0} \\ $$
