f-x-sin-sin-2-x-cos-sin-2-x-then-the-range-of-f-x-is-

Question Number 24042 by Tinkutara last updated on 11/Nov/17

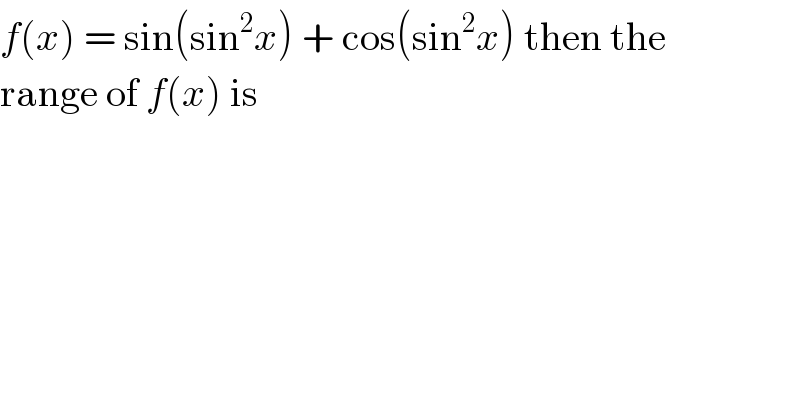
f (x) = \sin (\sin^{2} x) + \cos (\sin^{2} x) then the

range of f (x) is

Commented by mrW1 last updated on 11/Nov/17

[1, \sqrt{2}]

f (x) = \sin (\sin^{2} x) + \cos (\sin^{2} x)

= \sqrt{2} [\sin (\sin^{2} x) \cos \frac{π}{4} + \cos (\sin^{2} x) \sin \frac{π}{4}]

= \sqrt{2} \sin (\sin^{2} x + \frac{π}{4})

\sin (\sin^{2} x + \frac{π}{4}) ⩾ \sin \frac{π}{4} = \frac{1}{\sqrt{2}}

\sin (\sin^{2} x + \frac{π}{4}) ⩽ 1

\Rightarrow 1 ⩽ f (x) ⩽ \sqrt{2}

Commented by Tinkutara last updated on 12/Nov/17

Thank you very much Sir!

Answered by chowdhuryashis last updated on 11/Nov/17

[- 2, 2]

Commented by Tinkutara last updated on 12/Nov/17

Wrong .