Menu Close

f-x-sin-x-sec-x-1-xtan-x-find-f-x-

Tinku Tara 0 Comments
Pin




Question Number 25034 by chernoaguero@gmail.com last updated on 02/Dec/17
f(x)=((sin x+sec x)/(1+xtan x)) find f′(x)
$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{sin}\:\mathrm{x}+\mathrm{sec}\:\mathrm{x}}{\mathrm{1}+\mathrm{xtan}\:\mathrm{x}} \\ $$$$ \\ $$$$\mathrm{find}\:\mathrm{f}'\left(\mathrm{x}\right) \\ $$
Answered by prakash jain last updated on 02/Dec/17
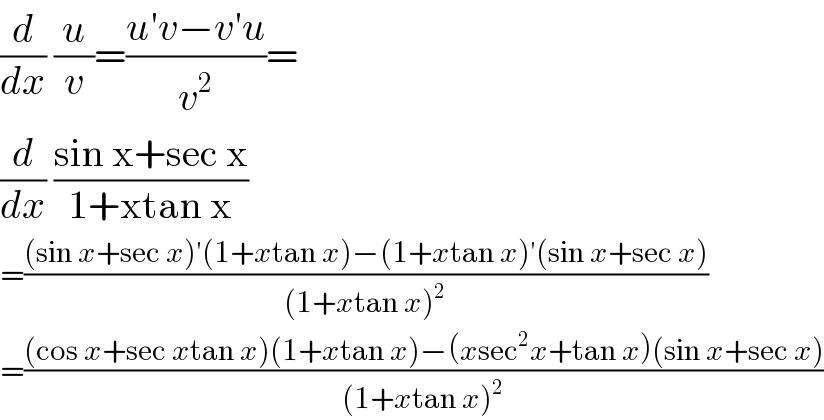
(d/dx) (u/v)=((u′v−v′u)/v^2 )= (d/dx) ((sin x+sec x)/(1+xtan x)) =(((sin x+sec x)′(1+xtan x)−(1+xtan x)′(sin x+sec x))/((1+xtan x)^2 )) =(((cos x+sec xtan x)(1+xtan x)−(xsec^2 x+tan x)(sin x+sec x))/((1+xtan x)^2 ))
$$\frac{{d}}{{dx}}\:\frac{{u}}{{v}}=\frac{{u}'{v}−{v}'{u}}{{v}^{\mathrm{2}} }= \\ $$$$\frac{{d}}{{dx}}\:\frac{\mathrm{sin}\:\mathrm{x}+\mathrm{sec}\:\mathrm{x}}{\mathrm{1}+\mathrm{xtan}\:\mathrm{x}} \\ $$$$=\frac{\left(\mathrm{sin}\:{x}+\mathrm{sec}\:{x}\right)'\left(\mathrm{1}+{x}\mathrm{tan}\:{x}\right)−\left(\mathrm{1}+{x}\mathrm{tan}\:{x}\right)'\left(\mathrm{sin}\:{x}+\mathrm{sec}\:{x}\right)}{\left(\mathrm{1}+{x}\mathrm{tan}\:{x}\right)^{\mathrm{2}} } \\ $$$$=\frac{\left(\mathrm{cos}\:{x}+\mathrm{sec}\:{x}\mathrm{tan}\:{x}\right)\left(\mathrm{1}+{x}\mathrm{tan}\:{x}\right)−\left({x}\mathrm{sec}^{\mathrm{2}} {x}+\mathrm{tan}\:{x}\right)\left(\mathrm{sin}\:{x}+\mathrm{sec}\:{x}\right)}{\left(\mathrm{1}+{x}\mathrm{tan}\:{x}\right)^{\mathrm{2}} } \\ $$
Commented by chernoaguero@gmail.com last updated on 02/Dec/17
Sir is there any trigonometric identity between them
$$\mathrm{Sir}\:\mathrm{is}\:\mathrm{there}\:\mathrm{any}\:\mathrm{trigonometric}\:\mathrm{identity}\:\mathrm{between}\:\mathrm{them} \\ $$
Commented by prakash jain last updated on 02/Dec/17
I didn′t simplify it further but will do it later today.
$$\mathrm{I}\:\mathrm{didn}'\mathrm{t}\:\mathrm{simplify}\:\mathrm{it}\:\mathrm{further}\:\mathrm{but}\:\mathrm{will}\:\mathrm{do} \\ $$$$\mathrm{it}\:\mathrm{later}\:\mathrm{today}. \\ $$
Commented by chernoaguero@gmail.com last updated on 02/Dec/17
Ok sir
$$\mathrm{Ok}\:\mathrm{sir}\: \\ $$
Answered by ajfour last updated on 02/Dec/17
y(1+xtan x)=sin x+(1/(cos x)) ⇒ y(cot x+x)=cosx+cosec x f ′(x)(cot x+x)−ycot^2 x= −sin x−cosec xcot x f ′(x)(cot x+x)=(((cos x+cosec x)cot^2 x)/((cot x+x))) −(sin x+cosec xcot x) f ′(x)=((cos xcot^2 x−cos x−xsin x−xcosec xcot x)/((cot x+x)^2 )) .
$${y}\left(\mathrm{1}+{x}\mathrm{tan}\:{x}\right)=\mathrm{sin}\:{x}+\frac{\mathrm{1}}{\mathrm{cos}\:{x}} \\ $$$$\Rightarrow\:{y}\left(\mathrm{cot}\:{x}+{x}\right)=\mathrm{cos}{x}+\mathrm{cosec}\:{x} \\ $$$${f}\:'\left({x}\right)\left(\mathrm{cot}\:{x}+{x}\right)−{y}\mathrm{cot}\:^{\mathrm{2}} {x}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{sin}\:{x}−\mathrm{cosec}\:{x}\mathrm{cot}\:{x} \\ $$$${f}\:'\left({x}\right)\left(\mathrm{cot}\:{x}+{x}\right)=\frac{\left(\mathrm{cos}\:{x}+\mathrm{cosec}\:{x}\right)\mathrm{cot}\:^{\mathrm{2}} {x}}{\left(\mathrm{cot}\:{x}+{x}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\left(\mathrm{sin}\:{x}+\mathrm{cosec}\:{x}\mathrm{cot}\:{x}\right) \\ $$$${f}\:'\left({x}\right)=\frac{\mathrm{cos}\:{x}\mathrm{cot}\:^{\mathrm{2}} {x}−\mathrm{cos}\:{x}−{x}\mathrm{sin}\:{x}−{x}\mathrm{cosec}\:{x}\mathrm{cot}\:{x}}{\left(\mathrm{cot}\:{x}+{x}\right)^{\mathrm{2}} }\:. \\ $$
Commented by chernoaguero@gmail.com last updated on 02/Dec/17
Thank u vry much sir
$$\mathrm{Thank}\:\mathrm{u}\:\mathrm{vry}\:\mathrm{much}\:\mathrm{sir}\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *