Question Number 125165 by Mammadli last updated on 08/Dec/20

$$\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)=\boldsymbol{{sinx}}^{\boldsymbol{{cosx}}} \\ $$$$\boldsymbol{{f}}\:'\left(\boldsymbol{{x}}\right)=? \\ $$
Answered by Dwaipayan Shikari last updated on 08/Dec/20
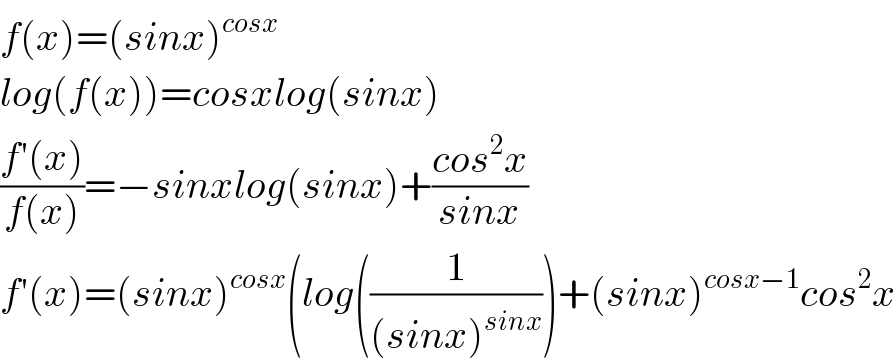
$${f}\left({x}\right)=\left({sinx}\right)^{{cosx}} \\ $$$${log}\left({f}\left({x}\right)\right)={cosxlog}\left({sinx}\right) \\ $$$$\frac{{f}'\left({x}\right)}{{f}\left({x}\right)}=−{sinxlog}\left({sinx}\right)+\frac{{cos}^{\mathrm{2}} {x}}{{sinx}} \\ $$$${f}'\left({x}\right)=\left({sinx}\right)^{{cosx}} \left({log}\left(\frac{\mathrm{1}}{\left({sinx}\right)^{{sinx}} }\right)+\left({sinx}\right)^{{cosx}−\mathrm{1}} {cos}^{\mathrm{2}} {x}\right. \\ $$
