Question Number 128370 by mathocean1 last updated on 06/Jan/21
![f(x)=(x−1)(√(x−1)) on ]1;+∞[ F(x)=?](https://www.tinkutara.com/question/Q128370.png)
$$\left.{f}\left({x}\right)=\left({x}−\mathrm{1}\right)\sqrt{{x}−\mathrm{1}}\:{on}\:\:\right]\mathrm{1};+\infty\left[\right. \\ $$$${F}\left({x}\right)=? \\ $$
Answered by mathmax by abdo last updated on 06/Jan/21
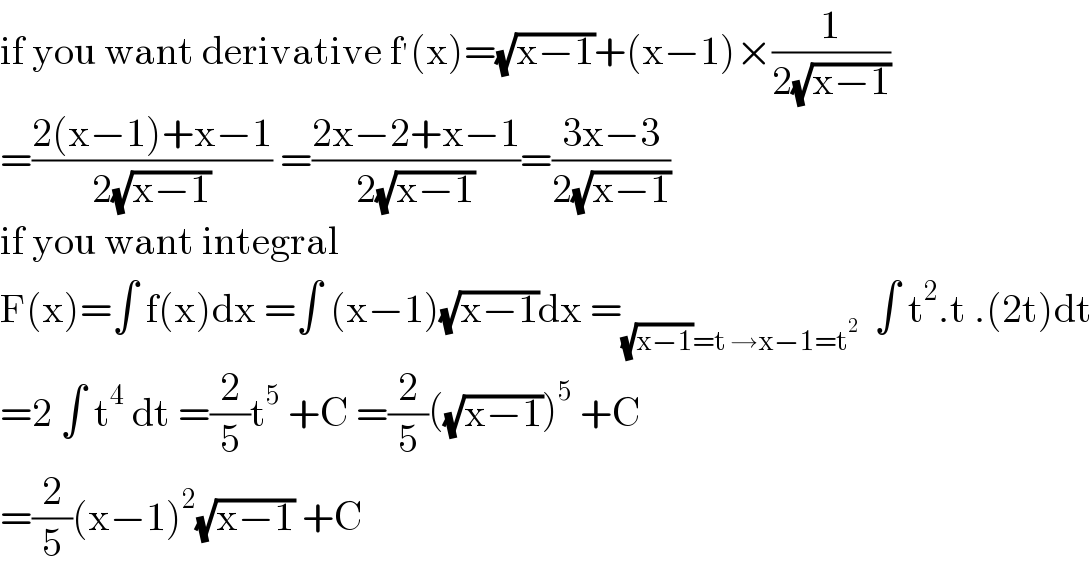
$$\mathrm{if}\:\mathrm{you}\:\mathrm{want}\:\mathrm{derivative}\:\mathrm{f}^{'} \left(\mathrm{x}\right)=\sqrt{\mathrm{x}−\mathrm{1}}+\left(\mathrm{x}−\mathrm{1}\right)×\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}−\mathrm{1}}} \\ $$$$=\frac{\mathrm{2}\left(\mathrm{x}−\mathrm{1}\right)+\mathrm{x}−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}−\mathrm{1}}}\:=\frac{\mathrm{2x}−\mathrm{2}+\mathrm{x}−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}−\mathrm{1}}}=\frac{\mathrm{3x}−\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{x}−\mathrm{1}}} \\ $$$$\mathrm{if}\:\mathrm{you}\:\mathrm{want}\:\mathrm{integral} \\ $$$$\mathrm{F}\left(\mathrm{x}\right)=\int\:\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}\:=\int\:\left(\mathrm{x}−\mathrm{1}\right)\sqrt{\mathrm{x}−\mathrm{1}}\mathrm{dx}\:=_{\sqrt{\mathrm{x}−\mathrm{1}}=\mathrm{t}\:\rightarrow\mathrm{x}−\mathrm{1}=\mathrm{t}^{\mathrm{2}} } \:\:\int\:\mathrm{t}^{\mathrm{2}} .\mathrm{t}\:.\left(\mathrm{2t}\right)\mathrm{dt} \\ $$$$=\mathrm{2}\:\int\:\mathrm{t}^{\mathrm{4}} \:\mathrm{dt}\:=\frac{\mathrm{2}}{\mathrm{5}}\mathrm{t}^{\mathrm{5}} \:+\mathrm{C}\:=\frac{\mathrm{2}}{\mathrm{5}}\left(\sqrt{\mathrm{x}−\mathrm{1}}\right)^{\mathrm{5}} \:+\mathrm{C} \\ $$$$=\frac{\mathrm{2}}{\mathrm{5}}\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} \sqrt{\mathrm{x}−\mathrm{1}}\:+\mathrm{C} \\ $$
