Question Number 29777 by Joel578 last updated on 12/Feb/18
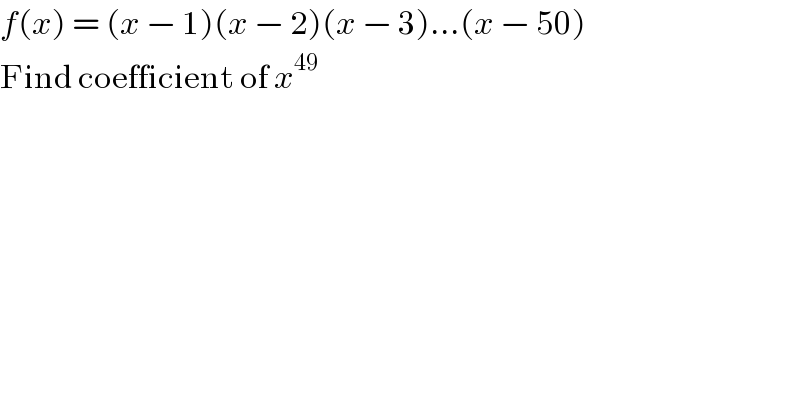
$${f}\left({x}\right)\:=\:\left({x}\:−\:\mathrm{1}\right)\left({x}\:−\:\mathrm{2}\right)\left({x}\:−\:\mathrm{3}\right)…\left({x}\:−\:\mathrm{50}\right) \\ $$$$\mathrm{Find}\:\mathrm{coefficient}\:\mathrm{of}\:{x}^{\mathrm{49}} \\ $$
Commented by mrW2 last updated on 12/Feb/18

$${see}\:{Q}\mathrm{29805} \\ $$
Commented by 803jaideep@gmail.com last updated on 12/Feb/18
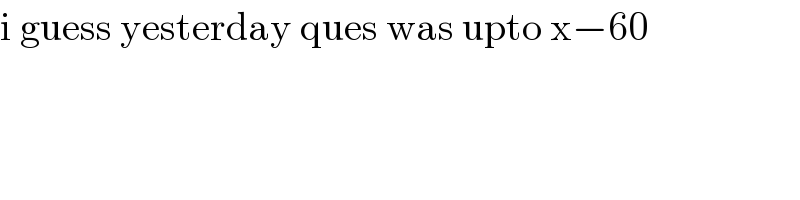
$$\mathrm{i}\:\mathrm{guess}\:\mathrm{yesterday}\:\mathrm{ques}\:\mathrm{was}\:\mathrm{upto}\:\mathrm{x}−\mathrm{60} \\ $$
Commented by Joel578 last updated on 12/Feb/18
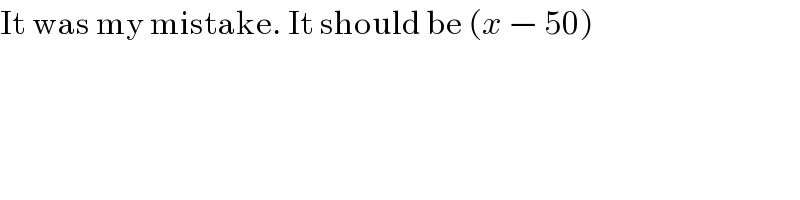
$$\mathrm{It}\:\mathrm{was}\:\mathrm{my}\:\mathrm{mistake}.\:\mathrm{It}\:\mathrm{should}\:\mathrm{be}\:\left({x}\:−\:\mathrm{50}\right) \\ $$
Commented by mrW2 last updated on 12/Feb/18
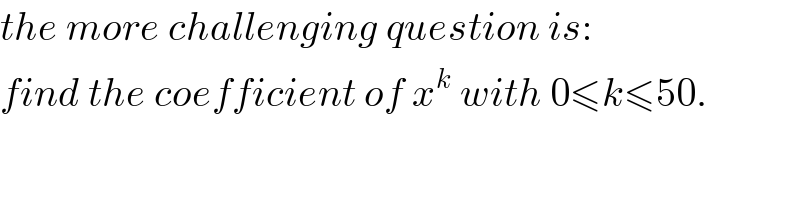
$${the}\:{more}\:{challenging}\:{question}\:{is}: \\ $$$${find}\:{the}\:{coefficient}\:{of}\:{x}^{{k}} \:{with}\:\mathrm{0}\leqslant{k}\leqslant\mathrm{50}. \\ $$
Commented by 803jaideep@gmail.com last updated on 12/Feb/18

$$\mathrm{thn}\:\mathrm{plz}\:\mathrm{take}\:\mathrm{an}\:\mathrm{example}\:\mathrm{and}\:\mathrm{make} \\ $$$$\mathrm{us}\:\mathrm{learn}\:\mathrm{about}\:\mathrm{some}\:\mathrm{mid}\:\mathrm{value}\:\mathrm{sir} \\ $$$$..\mathrm{like}\:\mathrm{30}\:\mathrm{or}\:\mathrm{25} \\ $$
Answered by puneet1789 last updated on 12/Feb/18
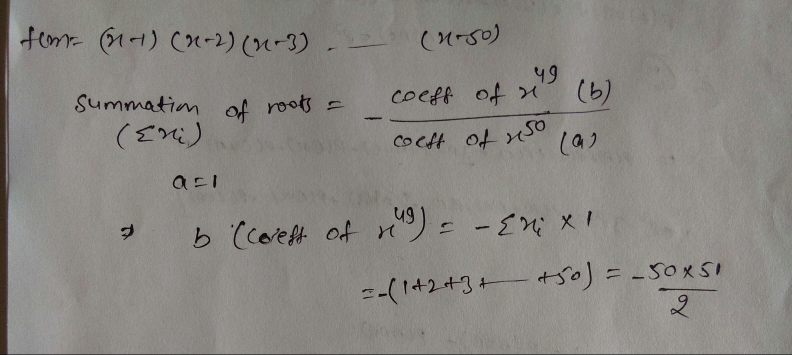
Commented by Joel578 last updated on 12/Feb/18
$${thank}\:{you}\:{very}\:{much} \\ $$
Answered by mrW2 last updated on 13/Feb/18

$${see}\:{Q}\mathrm{29805} \\ $$$${here}\:{n}=\mathrm{50} \\ $$$${a}_{{k}} =−{k},\:\mathrm{1}\leqslant{k}\leqslant\mathrm{50} \\ $$$${P}={a}_{\mathrm{1}} {a}_{\mathrm{2}} …{a}_{\mathrm{50}} =\mathrm{50}! \\ $$$$ \\ $$$${coefficient}\:{of}\:{x}^{\mathrm{49}} : \\ $$$${C}_{\mathrm{49}} =\underset{\mathrm{1}} {\overset{\mathrm{50}} {\sum}}{a}_{{i}} =−\left(\mathrm{1}+\mathrm{2}+…+\mathrm{50}\right)=−\frac{\mathrm{50}×\mathrm{51}}{\mathrm{2}}=−\mathrm{1275} \\ $$$$ \\ $$$${coefficient}\:{of}\:{x}^{\mathrm{30}} : \\ $$$${C}_{\mathrm{30}} =\frac{{P}}{\mathrm{1}×\mathrm{2}×\mathrm{3}…\mathrm{30}}+\frac{{P}}{\mathrm{1}×\mathrm{3}×\mathrm{4}…\mathrm{31}}+\frac{{P}}{\mathrm{1}×\mathrm{4}×\mathrm{5}…\mathrm{32}}+…+\frac{{P}}{\mathrm{1}×\mathrm{22}×\mathrm{23}…\mathrm{50}} \\ $$$$+\frac{{P}}{\mathrm{2}×\mathrm{3}×\mathrm{4}…\mathrm{31}}+\frac{{P}}{\mathrm{2}×\mathrm{4}×\mathrm{5}…\mathrm{32}}+\frac{{P}}{\mathrm{2}×\mathrm{5}×\mathrm{6}…\mathrm{33}}+…+\frac{{P}}{\mathrm{2}×\mathrm{22}×\mathrm{23}…\mathrm{50}} \\ $$$$+\frac{{P}}{\mathrm{3}×\mathrm{4}×\mathrm{5}…\mathrm{32}}+\frac{{P}}{\mathrm{3}×\mathrm{5}×\mathrm{6}…\mathrm{33}}+\frac{{P}}{\mathrm{3}×\mathrm{6}×\mathrm{7}…\mathrm{34}}+…+\frac{{P}}{\mathrm{3}×\mathrm{22}×\mathrm{23}…\mathrm{50}} \\ $$$$…. \\ $$$$+\frac{{P}}{\mathrm{20}×\mathrm{21}×\mathrm{22}…\mathrm{49}}+\frac{{P}}{\mathrm{20}×\mathrm{22}×\mathrm{23}…\mathrm{50}} \\ $$$$+\frac{{P}}{\mathrm{21}×\mathrm{22}×\mathrm{23}…\mathrm{50}} \\ $$$$=….. \\ $$
