Question Number 174570 by blackmamba last updated on 04/Aug/22
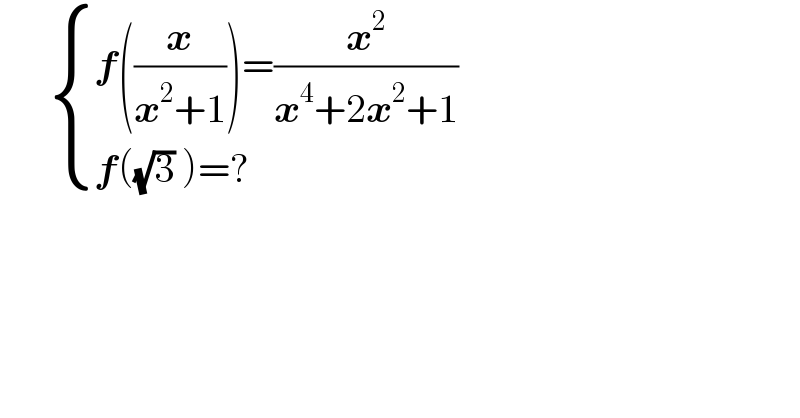
$$\:\:\:\:\:\:\begin{cases}{\boldsymbol{{f}}\left(\frac{\boldsymbol{{x}}}{\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{1}}\right)=\frac{\boldsymbol{{x}}^{\mathrm{2}} }{\boldsymbol{{x}}^{\mathrm{4}} +\mathrm{2}\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{1}}}\\{\boldsymbol{{f}}\left(\sqrt{\mathrm{3}}\:\right)=?}\end{cases} \\ $$
Commented by infinityaction last updated on 04/Aug/22
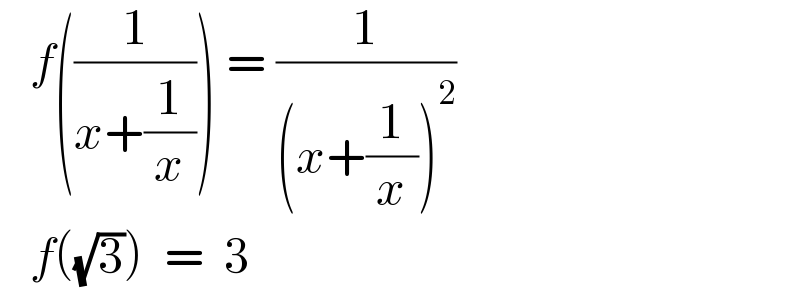
$$\:\:\:{f}\left(\frac{\mathrm{1}}{{x}+\frac{\mathrm{1}}{{x}}}\right)\:=\:\frac{\mathrm{1}}{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} } \\ $$$$\:\:\:{f}\left(\sqrt{\mathrm{3}}\right)\:\:=\:\:\mathrm{3} \\ $$
Answered by Rasheed.Sindhi last updated on 05/Aug/22
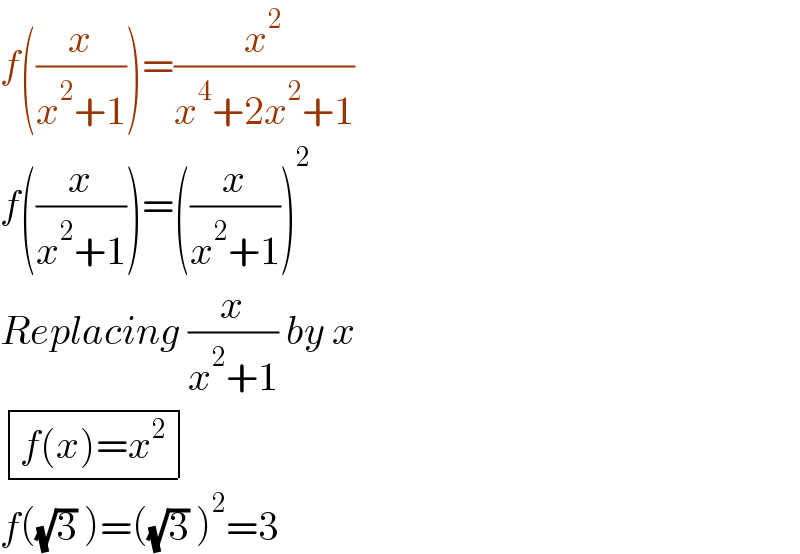
$${f}\left(\frac{{x}}{{x}^{\mathrm{2}} +\mathrm{1}}\right)=\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$${f}\left(\frac{{x}}{{x}^{\mathrm{2}} +\mathrm{1}}\right)=\left(\frac{{x}}{{x}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} \\ $$$${Replacing}\:\frac{{x}}{{x}^{\mathrm{2}} +\mathrm{1}}\:{by}\:{x} \\ $$$$\begin{array}{|c|}{{f}\left({x}\right)={x}^{\mathrm{2}} }\\\hline\end{array} \\ $$$${f}\left(\sqrt{\mathrm{3}}\:\right)=\left(\sqrt{\mathrm{3}}\:\right)^{\mathrm{2}} =\mathrm{3} \\ $$
