Question Number 108901 by ZiYangLee last updated on 20/Aug/20
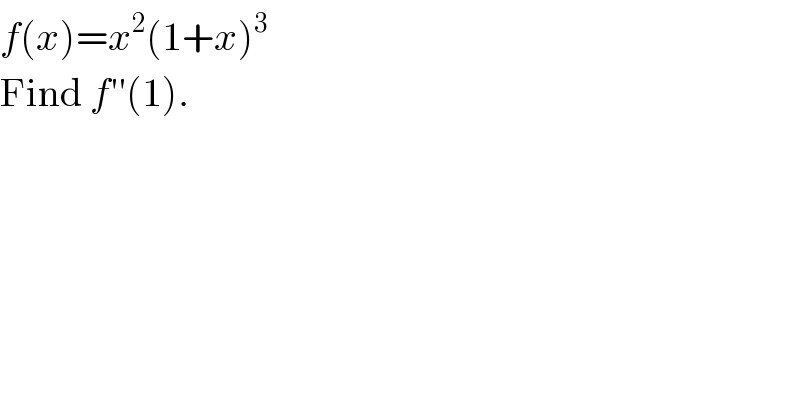
$${f}\left({x}\right)={x}^{\mathrm{2}} \left(\mathrm{1}+{x}\right)^{\mathrm{3}} \\ $$$$\mathrm{Find}\:{f}''\left(\mathrm{1}\right).\: \\ $$
Answered by malwaan last updated on 20/Aug/20
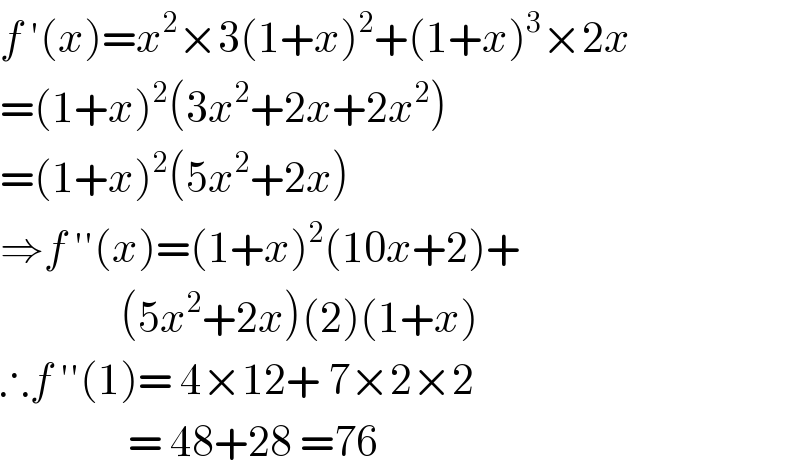
$${f}\:'\left({x}\right)={x}^{\mathrm{2}} ×\mathrm{3}\left(\mathrm{1}+{x}\right)^{\mathrm{2}} +\left(\mathrm{1}+{x}\right)^{\mathrm{3}} ×\mathrm{2}{x} \\ $$$$=\left(\mathrm{1}+{x}\right)^{\mathrm{2}} \left(\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}{x}^{\mathrm{2}} \right) \\ $$$$=\left(\mathrm{1}+{x}\right)^{\mathrm{2}} \left(\mathrm{5}{x}^{\mathrm{2}} +\mathrm{2}{x}\right) \\ $$$$\Rightarrow{f}\:''\left({x}\right)=\left(\mathrm{1}+{x}\right)^{\mathrm{2}} \left(\mathrm{10}{x}+\mathrm{2}\right)+ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{5}{x}^{\mathrm{2}} +\mathrm{2}{x}\right)\left(\mathrm{2}\right)\left(\mathrm{1}+{x}\right) \\ $$$$\therefore{f}\:''\left(\mathrm{1}\right)=\:\mathrm{4}×\mathrm{12}+\:\mathrm{7}×\mathrm{2}×\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{48}+\mathrm{28}\:=\mathrm{76} \\ $$
