Question Number 182581 by sciencestudent last updated on 11/Dec/22
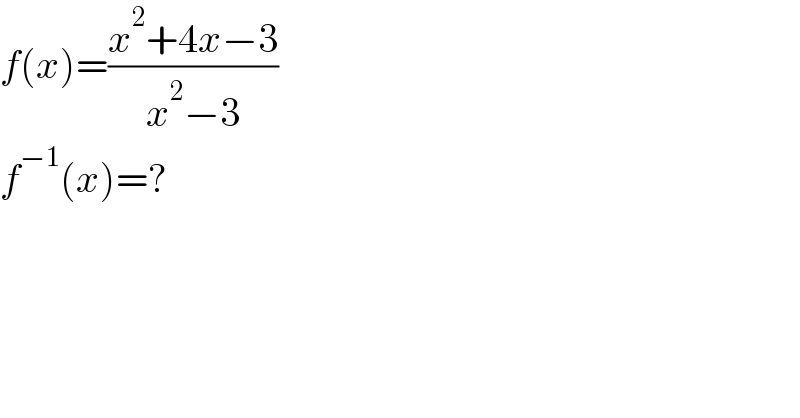
$${f}\left({x}\right)=\frac{{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{3}}{{x}^{\mathrm{2}} −\mathrm{3}}\:\:\: \\ $$$${f}^{−\mathrm{1}} \left({x}\right)=? \\ $$
Answered by cortano1 last updated on 11/Dec/22
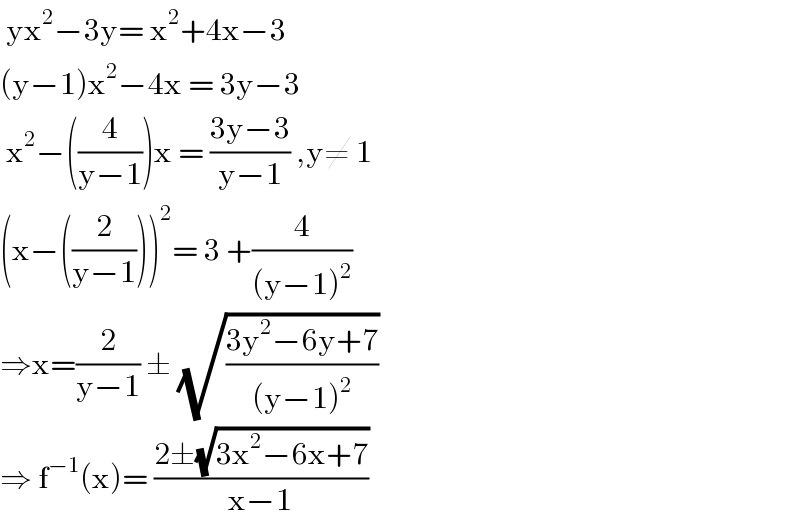
$$\:\mathrm{yx}^{\mathrm{2}} −\mathrm{3y}=\:\mathrm{x}^{\mathrm{2}} +\mathrm{4x}−\mathrm{3} \\ $$$$\left(\mathrm{y}−\mathrm{1}\right)\mathrm{x}^{\mathrm{2}} −\mathrm{4x}\:=\:\mathrm{3y}−\mathrm{3} \\ $$$$\:\mathrm{x}^{\mathrm{2}} −\left(\frac{\mathrm{4}}{\mathrm{y}−\mathrm{1}}\right)\mathrm{x}\:=\:\frac{\mathrm{3y}−\mathrm{3}}{\mathrm{y}−\mathrm{1}}\:,\mathrm{y}\neq\:\mathrm{1} \\ $$$$\left(\mathrm{x}−\left(\frac{\mathrm{2}}{\mathrm{y}−\mathrm{1}}\right)\right)^{\mathrm{2}} =\:\mathrm{3}\:+\frac{\mathrm{4}}{\left(\mathrm{y}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{x}=\frac{\mathrm{2}}{\mathrm{y}−\mathrm{1}}\:\pm\:\sqrt{\frac{\mathrm{3y}^{\mathrm{2}} −\mathrm{6y}+\mathrm{7}}{\left(\mathrm{y}−\mathrm{1}\right)^{\mathrm{2}} }} \\ $$$$\Rightarrow\:\mathrm{f}^{−\mathrm{1}} \left(\mathrm{x}\right)=\:\frac{\mathrm{2}\pm\sqrt{\mathrm{3x}^{\mathrm{2}} −\mathrm{6x}+\mathrm{7}}}{\mathrm{x}−\mathrm{1}} \\ $$
