Menu Close

f-x-x-2014-2x-2013-3x-2012-4x-2011-2014x-2015-min-f-x-

Tinku Tara 0 Comments
Pin




Question Number 157952 by cortano last updated on 30/Oct/21
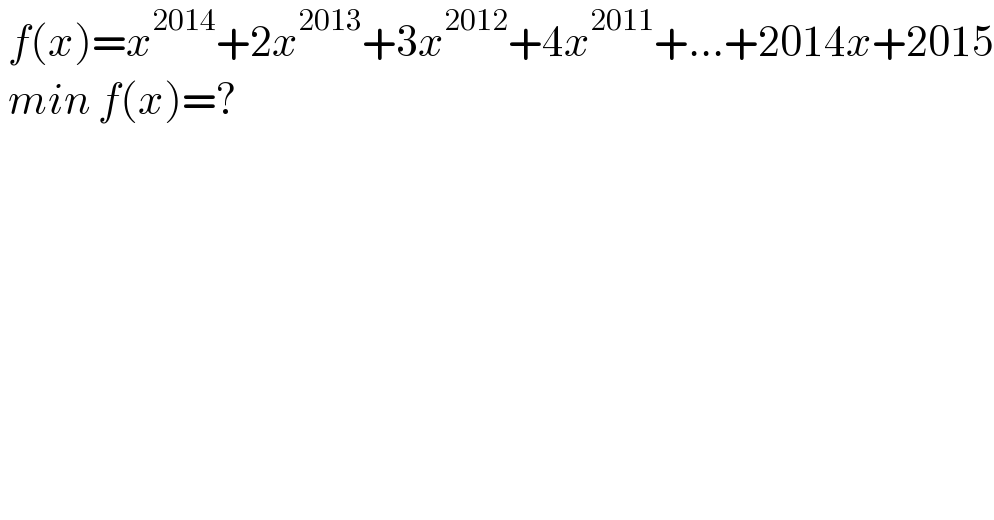
f(x)=x^(2014) +2x^(2013) +3x^(2012) +4x^(2011) +...+2014x+2015 min f(x)=?
$$\:{f}\left({x}\right)={x}^{\mathrm{2014}} +\mathrm{2}{x}^{\mathrm{2013}} +\mathrm{3}{x}^{\mathrm{2012}} +\mathrm{4}{x}^{\mathrm{2011}} +…+\mathrm{2014}{x}+\mathrm{2015} \\ $$$$\:{min}\:{f}\left({x}\right)=? \\ $$
Answered by aleks041103 last updated on 31/Oct/21
f(x)=Σ_(i=1) ^(2015) ix^(2015−i) =−x^(2016) Σ_(i=1) ^(2015) (−i)x^(−i−1) = =−x^(2016) (d/dx)(Σ_(i=1) ^(2015) x^(−i) ) Σ_(i=1) ^(2015) x^(−i) =(1/x)Σ_(i=0) ^(2014) ((1/x))^i =(1/x) ((((1/x))^(2015) −1)/((1/x)−1))= =−((x^(−2015) −1)/(x−1)) ⇒f(x)=−x^(2016) (d/dx)(((1−x^(−2015) )/(x−1)))= =−x^(2016) ((2015x^(−2016) (x−1)−1+x^(−2015) )/((x−1)^2 ))= =−((2015(x−1)−x^(2016) +x)/((x−1)^2 ))=((x^(2016) −2016x+2015)/((x−1)^2 )) ⇒f(x)=((x^(2016) −2016x+2015)/((x−1)^2 )) f′(x)=(((2016x^(2015) −2016)(x−1)^2 −2(x−1)(x^(2016) −2016x+2015))/((x−1)^4 ))= =((2016(x^(2015) −1)(x−1)−2x^(2016) +2.2016x−2.2015)/((x−1)^3 ))= =((2016(x^(2016) −x^(2015) −x+1)−2x^(2016) +2.2016x−2.2015)/((x−1)^3 ))= =((2014x^(2016) −2016x^(2015) +2016x−2014)/((x−1)^3 )) For extremum we need f′=0⇒ 2014x^(2016) −2016x^(2015) +2016x−2014=0 This polynome has only 2 real solutions: x=+1;−1. f′(1)=lim_(x→1) ((2014x^(2016) −2016x^(2015) +2016x−2014)/((x−1)^3 ))= L′H= lim_(x→1) ((2016(2014x^(2015) −2015x^(2014) +1))/(3(x−1)^2 ))= L′H=((2016)/3)lim_(x→1) ((2015.2014x^(2013) (x−1))/(2(x−1)))= =((2016.2015.2014)/6)≠0 ⇒This leaves for possible extrema only x=−1 It can be easily seen that: lim_(x→±∞) f(x)→+∞ Then f(x) can only have a minimum at x=−1. Then the answer will be: min(f)=f(−1)=(((−1)^(2016) −2016(−1)+2015)/((−1−1)^2 ))= =((1+2016+2015)/4)=1008 ⇒min(f)=1008
$${f}\left({x}\right)=\underset{{i}=\mathrm{1}} {\overset{\mathrm{2015}} {\sum}}{ix}^{\mathrm{2015}−{i}} =−{x}^{\mathrm{2016}} \underset{{i}=\mathrm{1}} {\overset{\mathrm{2015}} {\sum}}\left(−{i}\right){x}^{−{i}−\mathrm{1}} = \\ $$$$=−{x}^{\mathrm{2016}} \frac{{d}}{{dx}}\left(\underset{{i}=\mathrm{1}} {\overset{\mathrm{2015}} {\sum}}{x}^{−{i}} \right) \\ $$$$\underset{{i}=\mathrm{1}} {\overset{\mathrm{2015}} {\sum}}{x}^{−{i}} =\frac{\mathrm{1}}{{x}}\underset{{i}=\mathrm{0}} {\overset{\mathrm{2014}} {\sum}}\left(\frac{\mathrm{1}}{{x}}\right)^{{i}} =\frac{\mathrm{1}}{{x}}\:\frac{\left(\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2015}} −\mathrm{1}}{\frac{\mathrm{1}}{{x}}−\mathrm{1}}= \\ $$$$=−\frac{{x}^{−\mathrm{2015}} −\mathrm{1}}{{x}−\mathrm{1}} \\ $$$$\Rightarrow{f}\left({x}\right)=−{x}^{\mathrm{2016}} \frac{{d}}{{dx}}\left(\frac{\mathrm{1}−{x}^{−\mathrm{2015}} }{{x}−\mathrm{1}}\right)= \\ $$$$=−{x}^{\mathrm{2016}} \frac{\mathrm{2015}{x}^{−\mathrm{2016}} \left({x}−\mathrm{1}\right)−\mathrm{1}+{x}^{−\mathrm{2015}} }{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }= \\ $$$$=−\frac{\mathrm{2015}\left({x}−\mathrm{1}\right)−{x}^{\mathrm{2016}} +{x}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }=\frac{{x}^{\mathrm{2016}} −\mathrm{2016}{x}+\mathrm{2015}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow{f}\left({x}\right)=\frac{{x}^{\mathrm{2016}} −\mathrm{2016}{x}+\mathrm{2015}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${f}'\left({x}\right)=\frac{\left(\mathrm{2016}{x}^{\mathrm{2015}} −\mathrm{2016}\right)\left({x}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2016}} −\mathrm{2016}{x}+\mathrm{2015}\right)}{\left({x}−\mathrm{1}\right)^{\mathrm{4}} }= \\ $$$$=\frac{\mathrm{2016}\left({x}^{\mathrm{2015}} −\mathrm{1}\right)\left({x}−\mathrm{1}\right)−\mathrm{2}{x}^{\mathrm{2016}} +\mathrm{2}.\mathrm{2016}{x}−\mathrm{2}.\mathrm{2015}}{\left({x}−\mathrm{1}\right)^{\mathrm{3}} }= \\ $$$$=\frac{\mathrm{2016}\left({x}^{\mathrm{2016}} −{x}^{\mathrm{2015}} −{x}+\mathrm{1}\right)−\mathrm{2}{x}^{\mathrm{2016}} +\mathrm{2}.\mathrm{2016}{x}−\mathrm{2}.\mathrm{2015}}{\left({x}−\mathrm{1}\right)^{\mathrm{3}} }= \\ $$$$=\frac{\mathrm{2014}{x}^{\mathrm{2016}} −\mathrm{2016}{x}^{\mathrm{2015}} +\mathrm{2016}{x}−\mathrm{2014}}{\left({x}−\mathrm{1}\right)^{\mathrm{3}} } \\ $$$${For}\:{extremum}\:{we}\:{need}\:{f}'=\mathrm{0}\Rightarrow \\ $$$$\mathrm{2014}{x}^{\mathrm{2016}} −\mathrm{2016}{x}^{\mathrm{2015}} +\mathrm{2016}{x}−\mathrm{2014}=\mathrm{0} \\ $$$${This}\:{polynome}\:{has}\:{only}\:\mathrm{2}\:{real}\:{solutions}: \\ $$$${x}=+\mathrm{1};−\mathrm{1}. \\ $$$${f}'\left(\mathrm{1}\right)=\underset{{x}\rightarrow\mathrm{1}} {{lim}}\frac{\mathrm{2014}{x}^{\mathrm{2016}} −\mathrm{2016}{x}^{\mathrm{2015}} +\mathrm{2016}{x}−\mathrm{2014}}{\left({x}−\mathrm{1}\right)^{\mathrm{3}} }= \\ $$$${L}'{H}=\:\underset{{x}\rightarrow\mathrm{1}} {{lim}}\frac{\mathrm{2016}\left(\mathrm{2014}{x}^{\mathrm{2015}} −\mathrm{2015}{x}^{\mathrm{2014}} +\mathrm{1}\right)}{\mathrm{3}\left({x}−\mathrm{1}\right)^{\mathrm{2}} }= \\ $$$${L}'{H}=\frac{\mathrm{2016}}{\mathrm{3}}\underset{{x}\rightarrow\mathrm{1}} {{lim}}\frac{\mathrm{2015}.\mathrm{2014}{x}^{\mathrm{2013}} \left({x}−\mathrm{1}\right)}{\mathrm{2}\left({x}−\mathrm{1}\right)}= \\ $$$$=\frac{\mathrm{2016}.\mathrm{2015}.\mathrm{2014}}{\mathrm{6}}\neq\mathrm{0} \\ $$$$\Rightarrow{This}\:{leaves}\:{for}\:{possible}\:{extrema}\:{only}\:{x}=−\mathrm{1} \\ $$$${It}\:{can}\:{be}\:{easily}\:{seen}\:{that}: \\ $$$$\underset{{x}\rightarrow\pm\infty} {{lim}}\:{f}\left({x}\right)\rightarrow+\infty \\ $$$${Then}\:{f}\left({x}\right)\:{can}\:{only}\:{have}\:{a}\:{minimum} \\ $$$${at}\:{x}=−\mathrm{1}. \\ $$$${Then}\:{the}\:{answer}\:{will}\:{be}: \\ $$$${min}\left({f}\right)={f}\left(−\mathrm{1}\right)=\frac{\left(−\mathrm{1}\right)^{\mathrm{2016}} −\mathrm{2016}\left(−\mathrm{1}\right)+\mathrm{2015}}{\left(−\mathrm{1}−\mathrm{1}\right)^{\mathrm{2}} }= \\ $$$$=\frac{\mathrm{1}+\mathrm{2016}+\mathrm{2015}}{\mathrm{4}}=\mathrm{1008} \\ $$$$\Rightarrow{min}\left({f}\right)=\mathrm{1008}\: \\ $$
Commented by aleks041103 last updated on 31/Oct/21
Additional: Solutions to the polynomial 2014x^(2016) −2016x^(2015) +2016x−2014=0 p(x)=2014x^(2016) −2016x^(2015) +2016x−2014 Solution: Let′s find the extremums p′=2016.2014x^(2015) −2016.2015x^(2014) +2016= =2016(2014x^(2015) −2015x^(2014) +1)=2016g(x) let′s analyze g(x): g′(x)=2014.2015x^(2013) (x−1) g(x) can have extrema only at x=0 and x=1. g′′(x)=2014.2015x^(2012) (2014x−2013) g′′(1)=2014.2015>0 ⇒g(1)=0 is a min of g(x) g^((n)) (x)=2014.2015D^((n−1)) (x^(2014) −x^(2013) )= =2014.2015(((2014!)/((2015−n)!))x^(2015−n) −((2013!)/((2014−n)!))x^(2014−n) ) ⇒g^((n)) (0)= { ((0, n=1,2,...,2013,2016,...)),((−2015!, n=2014)),((2014.2015!, n=2015)) :} Since the smallest n for which g^((n)) (0)≠0 is even, g(0)=1 is a max of g(x). By the graph of g(x), which we vaugely construct using the analysis we did on g(x), we see that there are 2 points where g(x)=0 − at x=1 and at some x=x_1 <0. Then p′(x=1;x_1 )=0. p′′(x)=2016.2015.2014(x^(2014) −x^(2013) ) Then at x_1 <0 we see that p′′(x)>0. Therefore p(x) has a minimum at x=x_1 . p′′(x=1)=0 p′′′(x)=2016.2015.2014x^(2012) (2014x−2013) ⇒p′′′(x=1)=2016.2015.2014>0 ⇒p(x) has a saddle point at x=1. Then we construct vaugely the graph of p(x) and we see, that p(x)=0 has only 2 solutions. They can be found by inspection: p(1)=p(−1)=0
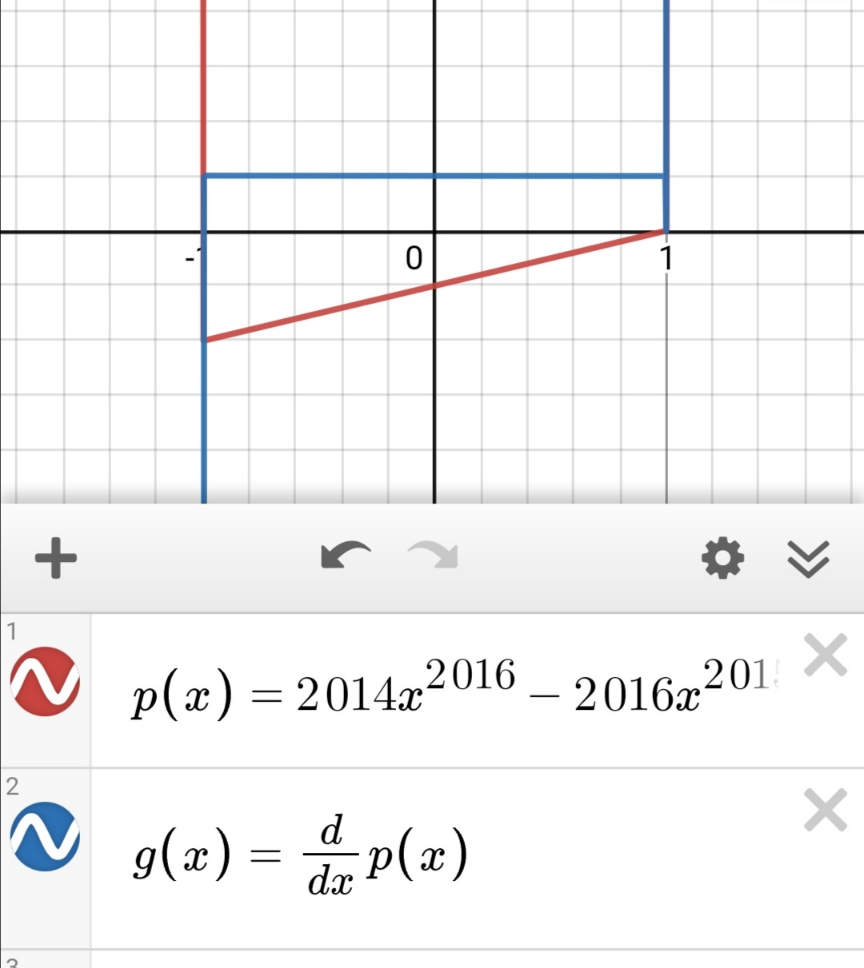
$${Additional}: \\ $$$${Solutions}\:{to}\:{the}\:{polynomial} \\ $$$$\mathrm{2014}{x}^{\mathrm{2016}} −\mathrm{2016}{x}^{\mathrm{2015}} +\mathrm{2016}{x}−\mathrm{2014}=\mathrm{0} \\ $$$${p}\left({x}\right)=\mathrm{2014}{x}^{\mathrm{2016}} −\mathrm{2016}{x}^{\mathrm{2015}} +\mathrm{2016}{x}−\mathrm{2014} \\ $$$${Solution}: \\ $$$${Let}'{s}\:{find}\:{the}\:{extremums} \\ $$$${p}'=\mathrm{2016}.\mathrm{2014}{x}^{\mathrm{2015}} −\mathrm{2016}.\mathrm{2015}{x}^{\mathrm{2014}} +\mathrm{2016}= \\ $$$$=\mathrm{2016}\left(\mathrm{2014}{x}^{\mathrm{2015}} −\mathrm{2015}{x}^{\mathrm{2014}} +\mathrm{1}\right)=\mathrm{2016}{g}\left({x}\right) \\ $$$$ \\ $$$${let}'{s}\:{analyze}\:{g}\left({x}\right): \\ $$$${g}'\left({x}\right)=\mathrm{2014}.\mathrm{2015}{x}^{\mathrm{2013}} \left({x}−\mathrm{1}\right) \\ $$$${g}\left({x}\right)\:{can}\:{have}\:{extrema}\:{only}\:{at}\:{x}=\mathrm{0}\:{and} \\ $$$${x}=\mathrm{1}. \\ $$$${g}''\left({x}\right)=\mathrm{2014}.\mathrm{2015}{x}^{\mathrm{2012}} \left(\mathrm{2014}{x}−\mathrm{2013}\right) \\ $$$${g}''\left(\mathrm{1}\right)=\mathrm{2014}.\mathrm{2015}>\mathrm{0} \\ $$$$\Rightarrow{g}\left(\mathrm{1}\right)=\mathrm{0}\:{is}\:{a}\:{min}\:{of}\:{g}\left({x}\right) \\ $$$${g}^{\left({n}\right)} \left({x}\right)=\mathrm{2014}.\mathrm{2015}{D}^{\left({n}−\mathrm{1}\right)} \left({x}^{\mathrm{2014}} −{x}^{\mathrm{2013}} \right)= \\ $$$$=\mathrm{2014}.\mathrm{2015}\left(\frac{\mathrm{2014}!}{\left(\mathrm{2015}−{n}\right)!}{x}^{\mathrm{2015}−{n}} −\frac{\mathrm{2013}!}{\left(\mathrm{2014}−{n}\right)!}{x}^{\mathrm{2014}−{n}} \right) \\ $$$$\Rightarrow{g}^{\left({n}\right)} \left(\mathrm{0}\right)=\begin{cases}{\mathrm{0},\:{n}=\mathrm{1},\mathrm{2},…,\mathrm{2013},\mathrm{2016},…}\\{−\mathrm{2015}!,\:{n}=\mathrm{2014}}\\{\mathrm{2014}.\mathrm{2015}!,\:{n}=\mathrm{2015}}\end{cases} \\ $$$${Since}\:{the}\:{smallest}\:{n}\:{for}\:{which}\:{g}^{\left({n}\right)} \left(\mathrm{0}\right)\neq\mathrm{0} \\ $$$${is}\:{even},\:{g}\left(\mathrm{0}\right)=\mathrm{1}\:{is}\:{a}\:{max}\:{of}\:{g}\left({x}\right). \\ $$$${By}\:{the}\:{graph}\:{of}\:{g}\left({x}\right),\:{which}\:{we}\:{vaugely}\:{construct}\: \\ $$$${using}\:{the}\:{analysis}\:{we}\:{did}\:{on}\:{g}\left({x}\right),\:{we}\:{see}\:{that}\:{there}\:{are}\: \\ $$$$\mathrm{2}\:{points}\:{where}\:{g}\left({x}\right)=\mathrm{0}\:−\:{at}\:{x}=\mathrm{1}\:{and}\:{at}\:{some}\:{x}={x}_{\mathrm{1}} <\mathrm{0}. \\ $$$$ \\ $$$${Then}\:{p}'\left({x}=\mathrm{1};{x}_{\mathrm{1}} \right)=\mathrm{0}. \\ $$$${p}''\left({x}\right)=\mathrm{2016}.\mathrm{2015}.\mathrm{2014}\left({x}^{\mathrm{2014}} −{x}^{\mathrm{2013}} \right) \\ $$$${Then}\:{at}\:{x}_{\mathrm{1}} <\mathrm{0}\:{we}\:{see}\:{that}\:{p}''\left({x}\right)>\mathrm{0}. \\ $$$${Therefore}\:{p}\left({x}\right)\:{has}\:{a}\:{minimum}\:{at}\:{x}={x}_{\mathrm{1}} . \\ $$$${p}''\left({x}=\mathrm{1}\right)=\mathrm{0} \\ $$$${p}'''\left({x}\right)=\mathrm{2016}.\mathrm{2015}.\mathrm{2014}{x}^{\mathrm{2012}} \left(\mathrm{2014}{x}−\mathrm{2013}\right) \\ $$$$\Rightarrow{p}'''\left({x}=\mathrm{1}\right)=\mathrm{2016}.\mathrm{2015}.\mathrm{2014}>\mathrm{0} \\ $$$$\Rightarrow{p}\left({x}\right)\:{has}\:{a}\:{saddle}\:{point}\:{at}\:{x}=\mathrm{1}. \\ $$$${Then}\:{we}\:{construct}\:{vaugely}\:{the}\:{graph}\:{of} \\ $$$${p}\left({x}\right)\:{and}\:{we}\:{see},\:{that}\:{p}\left({x}\right)=\mathrm{0}\:{has}\:{only} \\ $$$$\mathrm{2}\:{solutions}.\:{They}\:{can}\:{be}\:{found}\:{by}\:{inspection}: \\ $$$${p}\left(\mathrm{1}\right)={p}\left(−\mathrm{1}\right)=\mathrm{0} \\ $$
Commented by aleks041103 last updated on 31/Oct/21

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *