Menu Close

f-x-x-3-2x-4-f-1-x-

Tinku Tara 0 Comments
Pin




Question Number 54975 by naka3546 last updated on 15/Feb/19
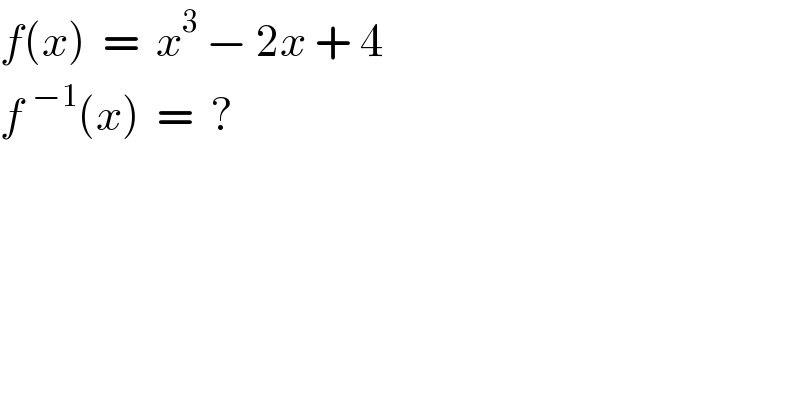
f(x) = x^3 − 2x + 4 f^(−1) (x) = ?
$${f}\left({x}\right)\:\:=\:\:{x}^{\mathrm{3}} \:−\:\mathrm{2}{x}\:+\:\mathrm{4} \\ $$$${f}\:^{−\mathrm{1}} \left({x}\right)\:\:=\:\:? \\ $$$$ \\ $$
Answered by mr W last updated on 15/Feb/19
y=x^3 −2x+4 x^3 −2x+4−y=0 (u+v)^3 −3uv(u+v)−(u^3 +v^3 )=0 ley x=u+v ⇒u^3 v^3 =(8/(27)) ⇒u^3 +v^3 =y−4 z^2 −(y−4)z+(8/(27))=0 z=(1/2)[y−4±(√(y^2 −8y+((400)/(27))))] u=(((y−4+(√(y^2 −8y+((400)/(27))))))^(1/3) /( (2)^(1/3) )) u=(((y−4−(√(y^2 −8y+((400)/(27))))))^(1/3) /( (2)^(1/3) )) ⇒x=u+v=((((y−4+(√(y^2 −8y+((400)/(27))))))^(1/3) +((y−4−(√(y^2 −8y+((400)/(27))))))^(1/3) )/( (2)^(1/3) )) ⇒f^(−1) (x)=((((x−4+(√(x^2 −8x+((400)/(27))))))^(1/3) +((x−4−(√(x^2 −8x+((400)/(27))))))^(1/3) )/( (2)^(1/3) ))
$${y}={x}^{\mathrm{3}} −\mathrm{2}{x}+\mathrm{4} \\ $$$${x}^{\mathrm{3}} −\mathrm{2}{x}+\mathrm{4}−{y}=\mathrm{0} \\ $$$$\left({u}+{v}\right)^{\mathrm{3}} −\mathrm{3}{uv}\left({u}+{v}\right)−\left({u}^{\mathrm{3}} +{v}^{\mathrm{3}} \right)=\mathrm{0} \\ $$$${ley}\:{x}={u}+{v} \\ $$$$\Rightarrow{u}^{\mathrm{3}} {v}^{\mathrm{3}} =\frac{\mathrm{8}}{\mathrm{27}} \\ $$$$\Rightarrow{u}^{\mathrm{3}} +{v}^{\mathrm{3}} ={y}−\mathrm{4} \\ $$$${z}^{\mathrm{2}} −\left({y}−\mathrm{4}\right){z}+\frac{\mathrm{8}}{\mathrm{27}}=\mathrm{0} \\ $$$${z}=\frac{\mathrm{1}}{\mathrm{2}}\left[{y}−\mathrm{4}\pm\sqrt{{y}^{\mathrm{2}} −\mathrm{8}{y}+\frac{\mathrm{400}}{\mathrm{27}}}\right] \\ $$$${u}=\frac{\sqrt[{\mathrm{3}}]{{y}−\mathrm{4}+\sqrt{{y}^{\mathrm{2}} −\mathrm{8}{y}+\frac{\mathrm{400}}{\mathrm{27}}}}}{\:\sqrt[{\mathrm{3}}]{\mathrm{2}}} \\ $$$${u}=\frac{\sqrt[{\mathrm{3}}]{{y}−\mathrm{4}−\sqrt{{y}^{\mathrm{2}} −\mathrm{8}{y}+\frac{\mathrm{400}}{\mathrm{27}}}}}{\:\sqrt[{\mathrm{3}}]{\mathrm{2}}} \\ $$$$\Rightarrow{x}={u}+{v}=\frac{\sqrt[{\mathrm{3}}]{{y}−\mathrm{4}+\sqrt{{y}^{\mathrm{2}} −\mathrm{8}{y}+\frac{\mathrm{400}}{\mathrm{27}}}}+\sqrt[{\mathrm{3}}]{{y}−\mathrm{4}−\sqrt{{y}^{\mathrm{2}} −\mathrm{8}{y}+\frac{\mathrm{400}}{\mathrm{27}}}}}{\:\sqrt[{\mathrm{3}}]{\mathrm{2}}} \\ $$$$\Rightarrow{f}^{−\mathrm{1}} \left({x}\right)=\frac{\sqrt[{\mathrm{3}}]{{x}−\mathrm{4}+\sqrt{{x}^{\mathrm{2}} −\mathrm{8}{x}+\frac{\mathrm{400}}{\mathrm{27}}}}+\sqrt[{\mathrm{3}}]{{x}−\mathrm{4}−\sqrt{{x}^{\mathrm{2}} −\mathrm{8}{x}+\frac{\mathrm{400}}{\mathrm{27}}}}}{\:\sqrt[{\mathrm{3}}]{\mathrm{2}}} \\ $$
Answered by MJS last updated on 15/Feb/19
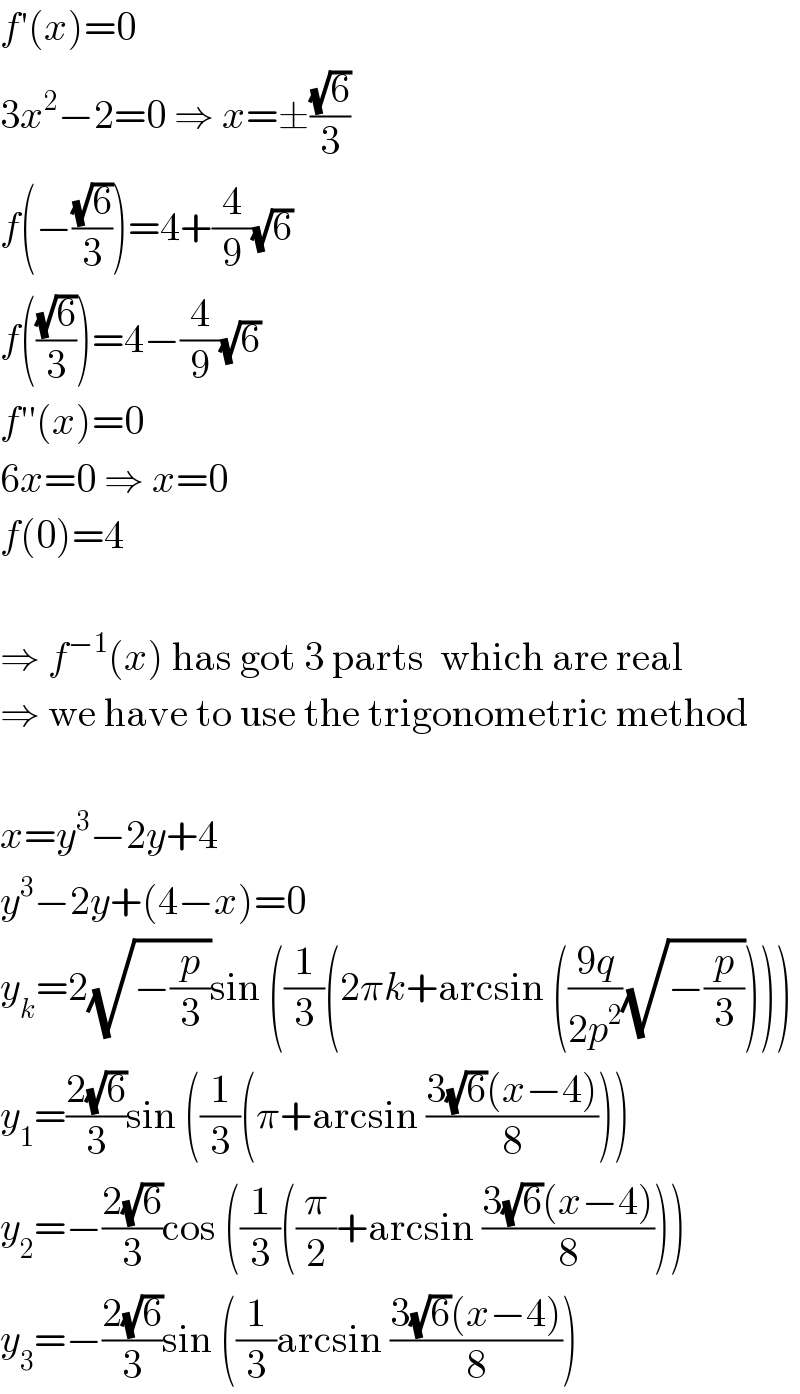
f′(x)=0 3x^2 −2=0 ⇒ x=±((√6)/3) f(−((√6)/3))=4+(4/9)(√6) f(((√6)/3))=4−(4/9)(√6) f′′(x)=0 6x=0 ⇒ x=0 f(0)=4 ⇒ f^(−1) (x) has got 3 parts which are real ⇒ we have to use the trigonometric method x=y^3 −2y+4 y^3 −2y+(4−x)=0 y_k =2(√(−(p/3)))sin ((1/3)(2πk+arcsin (((9q)/(2p^2 ))(√(−(p/3)))))) y_1 =((2(√6))/3)sin ((1/3)(π+arcsin ((3(√6)(x−4))/8))) y_2 =−((2(√6))/3)cos ((1/3)((π/2)+arcsin ((3(√6)(x−4))/8))) y_3 =−((2(√6))/3)sin ((1/3)arcsin ((3(√6)(x−4))/8))
$${f}'\left({x}\right)=\mathrm{0} \\ $$$$\mathrm{3}{x}^{\mathrm{2}} −\mathrm{2}=\mathrm{0}\:\Rightarrow\:{x}=\pm\frac{\sqrt{\mathrm{6}}}{\mathrm{3}} \\ $$$${f}\left(−\frac{\sqrt{\mathrm{6}}}{\mathrm{3}}\right)=\mathrm{4}+\frac{\mathrm{4}}{\mathrm{9}}\sqrt{\mathrm{6}} \\ $$$${f}\left(\frac{\sqrt{\mathrm{6}}}{\mathrm{3}}\right)=\mathrm{4}−\frac{\mathrm{4}}{\mathrm{9}}\sqrt{\mathrm{6}} \\ $$$${f}''\left({x}\right)=\mathrm{0} \\ $$$$\mathrm{6}{x}=\mathrm{0}\:\Rightarrow\:{x}=\mathrm{0} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{4} \\ $$$$ \\ $$$$\Rightarrow\:{f}^{−\mathrm{1}} \left({x}\right)\:\mathrm{has}\:\mathrm{got}\:\mathrm{3}\:\mathrm{parts}\:\:\mathrm{which}\:\mathrm{are}\:\mathrm{real} \\ $$$$\Rightarrow\:\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{use}\:\mathrm{the}\:\mathrm{trigonometric}\:\mathrm{method} \\ $$$$ \\ $$$${x}={y}^{\mathrm{3}} −\mathrm{2}{y}+\mathrm{4} \\ $$$${y}^{\mathrm{3}} −\mathrm{2}{y}+\left(\mathrm{4}−{x}\right)=\mathrm{0} \\ $$$${y}_{{k}} =\mathrm{2}\sqrt{−\frac{{p}}{\mathrm{3}}}\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{2}\pi{k}+\mathrm{arcsin}\:\left(\frac{\mathrm{9}{q}}{\mathrm{2}{p}^{\mathrm{2}} }\sqrt{−\frac{{p}}{\mathrm{3}}}\right)\right)\right) \\ $$$${y}_{\mathrm{1}} =\frac{\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{3}}\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\left(\pi+\mathrm{arcsin}\:\frac{\mathrm{3}\sqrt{\mathrm{6}}\left({x}−\mathrm{4}\right)}{\mathrm{8}}\right)\right) \\ $$$${y}_{\mathrm{2}} =−\frac{\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{3}}\mathrm{cos}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\pi}{\mathrm{2}}+\mathrm{arcsin}\:\frac{\mathrm{3}\sqrt{\mathrm{6}}\left({x}−\mathrm{4}\right)}{\mathrm{8}}\right)\right) \\ $$$${y}_{\mathrm{3}} =−\frac{\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{3}}\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\mathrm{3}\sqrt{\mathrm{6}}\left({x}−\mathrm{4}\right)}{\mathrm{8}}\right) \\ $$
Answered by Rio Mike last updated on 16/Feb/19
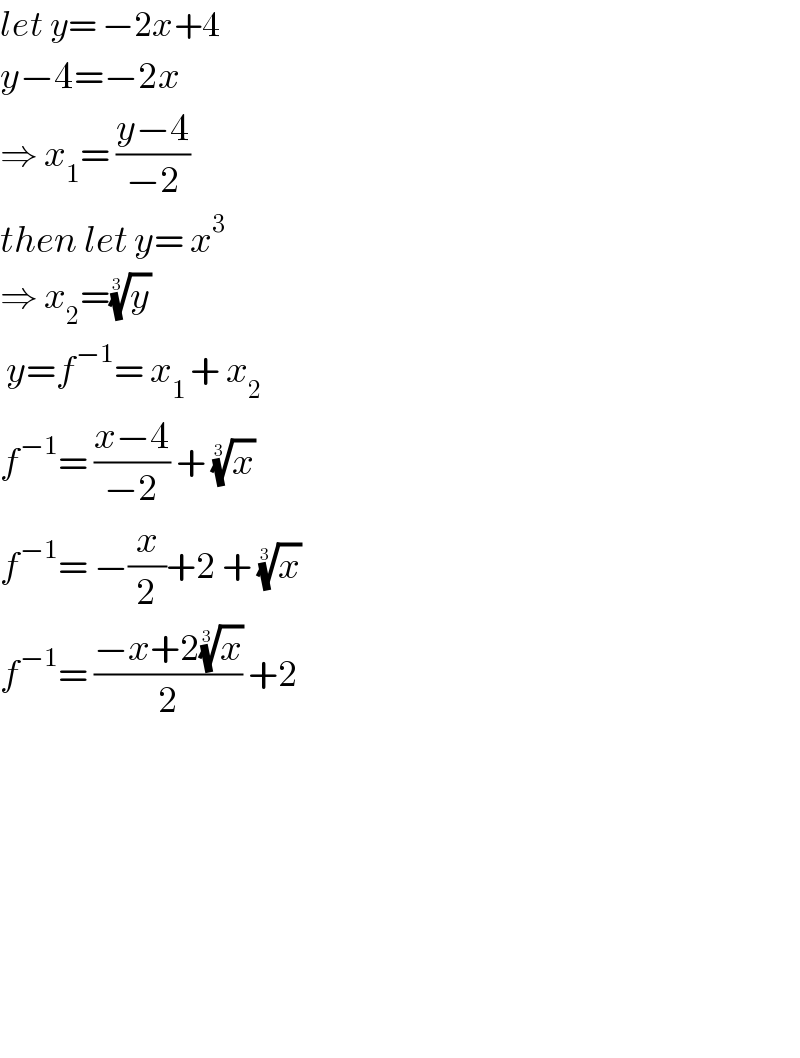
let y= −2x+4 y−4=−2x ⇒ x_1 = ((y−4)/(−2)) then let y= x^3 ⇒ x_2 =(y)^(1/3) y=f^(−1) = x_(1 ) + x_2 f^(−1) = ((x−4)/(−2)) + (x)^(1/3) f^(−1) = −(x/2)+2 + (x)^(1/3) f^(−1) = ((−x+2(x)^(1/3) )/2) +2
$${let}\:{y}=\:−\mathrm{2}{x}+\mathrm{4} \\ $$$${y}−\mathrm{4}=−\mathrm{2}{x} \\ $$$$\Rightarrow\:{x}_{\mathrm{1}} =\:\frac{{y}−\mathrm{4}}{−\mathrm{2}} \\ $$$${then}\:{let}\:{y}=\:{x}^{\mathrm{3}} \\ $$$$\Rightarrow\:{x}_{\mathrm{2}} =\sqrt[{\mathrm{3}}]{{y}}\: \\ $$$$\:{y}={f}^{−\mathrm{1}} =\:{x}_{\mathrm{1}\:} +\:{x}_{\mathrm{2}} \\ $$$${f}^{−\mathrm{1}} =\:\frac{{x}−\mathrm{4}}{−\mathrm{2}}\:+\:\sqrt[{\mathrm{3}}]{{x}}\: \\ $$$${f}^{−\mathrm{1}} =\:−\frac{{x}}{\mathrm{2}}+\mathrm{2}\:+\:\sqrt[{\mathrm{3}}]{{x}}\: \\ $$$${f}^{−\mathrm{1}} =\:\frac{−{x}+\mathrm{2}\sqrt[{\mathrm{3}}]{{x}}}{\mathrm{2}}\:+\mathrm{2}\:\: \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *