Question Number 93350 by abony1303 last updated on 12/May/20

$${f}\left({x}\right)={x}^{\mathrm{3}} +\mathrm{2}{x} \\ $$$${Find}:\:{f}^{−\mathrm{1}} \left({x}\right) \\ $$
Answered by Rio Michael last updated on 12/May/20
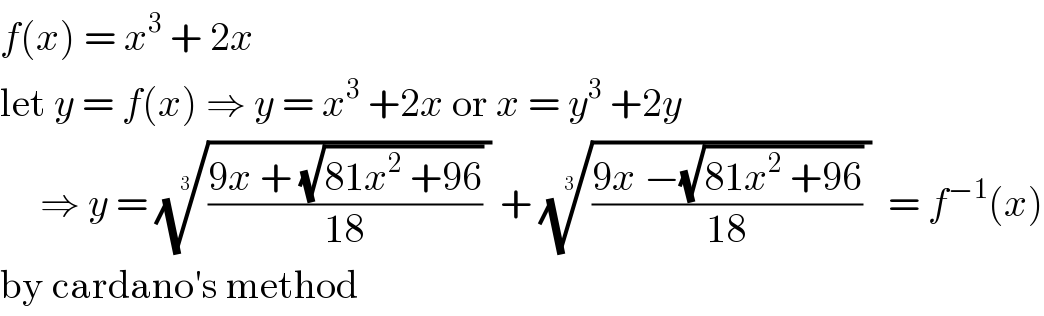
$${f}\left({x}\right)\:=\:{x}^{\mathrm{3}} \:+\:\mathrm{2}{x} \\ $$$$\mathrm{let}\:{y}\:=\:{f}\left({x}\right)\:\Rightarrow\:{y}\:=\:{x}^{\mathrm{3}} \:+\mathrm{2}{x}\:\mathrm{or}\:{x}\:=\:{y}^{\mathrm{3}} \:+\mathrm{2}{y} \\ $$$$\:\:\:\:\:\Rightarrow\:{y}\:=\:\sqrt[{\mathrm{3}}]{\frac{\mathrm{9}{x}\:+\:\sqrt{\mathrm{81}{x}^{\mathrm{2}} \:+\mathrm{96}}}{\mathrm{18}}\:}\:+\:\sqrt[{\mathrm{3}}]{\frac{\mathrm{9}{x}\:−\sqrt{\mathrm{81}{x}^{\mathrm{2}} \:+\mathrm{96}}}{\mathrm{18}}\:}\:\:=\:{f}^{−\mathrm{1}} \left({x}\right) \\ $$$$\mathrm{by}\:\mathrm{cardano}'\mathrm{s}\:\mathrm{method} \\ $$
