Question Number 184083 by mnjuly1970 last updated on 02/Jan/23
![f(x)= x^( 3) +3x^( 2) −ax is decreasing on [ −1 , 2] then which is correct... 1: [ −3 ,24] 2: [ 24 , +∞) 3: (−∞ ,−3] 4 :(−∞, −3]∪[24, +∞)](https://www.tinkutara.com/question/Q184083.png)
$$ \\ $$$$\:\:\:\:{f}\left({x}\right)=\:{x}^{\:\mathrm{3}} \:+\mathrm{3}{x}^{\:\mathrm{2}} −{ax}\:\:\:{is}\:\: \\ $$$$\:\:\:\:\:{decreasing}\:{on}\:\:\left[\:−\mathrm{1}\:,\:\mathrm{2}\right] \\ $$$$\:\:\:\:\:\:{then}\:\:{which}\:\:{is}\:{correct}… \\ $$$$\:\:\:\:\:\mathrm{1}:\:\:\:\left[\:−\mathrm{3}\:,\mathrm{24}\right] \\ $$$$\:\:\:\:\:\mathrm{2}:\:\:\left[\:\mathrm{24}\:,\:+\infty\right) \\ $$$$\:\:\:\:\:\:\mathrm{3}:\:\left(−\infty\:,−\mathrm{3}\right] \\ $$$$\:\:\:\:\:\:\:\:\mathrm{4}\::\left(−\infty,\:−\mathrm{3}\right]\cup\left[\mathrm{24},\:+\infty\right) \\ $$$$ \\ $$
Answered by mr W last updated on 02/Jan/23
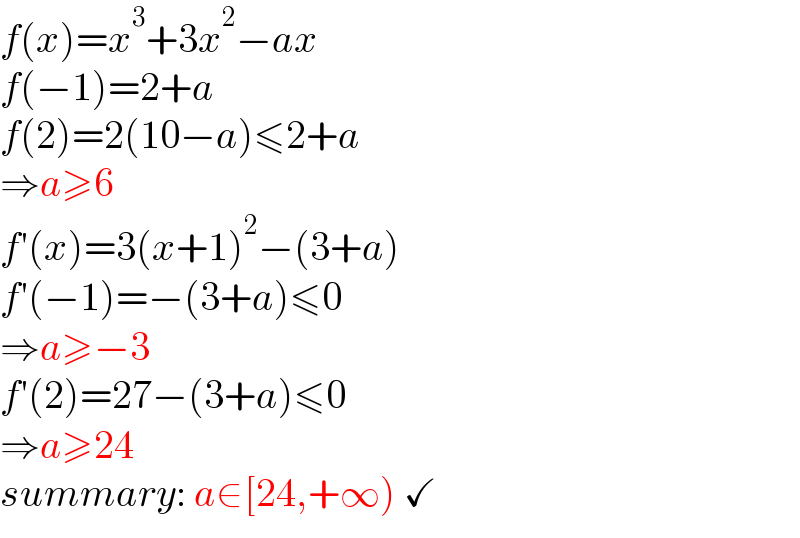
$${f}\left({x}\right)={x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} −{ax} \\ $$$${f}\left(−\mathrm{1}\right)=\mathrm{2}+{a} \\ $$$${f}\left(\mathrm{2}\right)=\mathrm{2}\left(\mathrm{10}−{a}\right)\leqslant\mathrm{2}+{a} \\ $$$$\Rightarrow{a}\geqslant\mathrm{6} \\ $$$${f}'\left({x}\right)=\mathrm{3}\left({x}+\mathrm{1}\right)^{\mathrm{2}} −\left(\mathrm{3}+{a}\right) \\ $$$${f}'\left(−\mathrm{1}\right)=−\left(\mathrm{3}+{a}\right)\leqslant\mathrm{0} \\ $$$$\Rightarrow{a}\geqslant−\mathrm{3} \\ $$$${f}'\left(\mathrm{2}\right)=\mathrm{27}−\left(\mathrm{3}+{a}\right)\leqslant\mathrm{0} \\ $$$$\Rightarrow{a}\geqslant\mathrm{24} \\ $$$${summary}:\:{a}\in\left[\mathrm{24},+\infty\right)\:\checkmark \\ $$
Commented by mnjuly1970 last updated on 04/Jan/23
$${peace}\:{be}\:{upon}\:{you}\:{sir}\:{w} \\ $$
Commented by mr W last updated on 04/Jan/23

$${thanks}\:{sir}! \\ $$
