Question Number 85238 by naka3546 last updated on 20/Mar/20
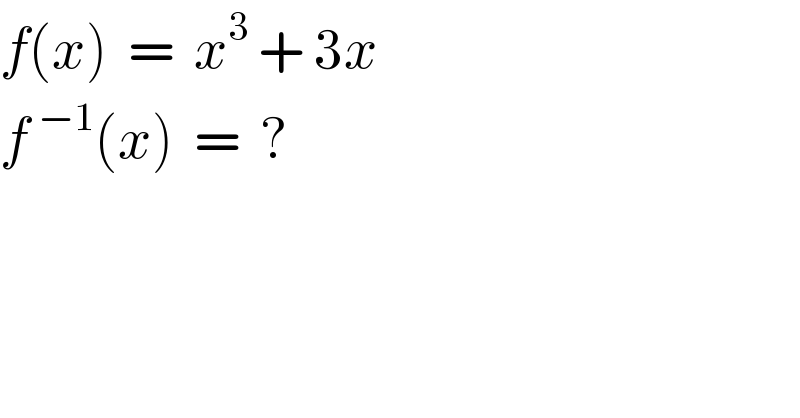
$${f}\left({x}\right)\:\:=\:\:{x}^{\mathrm{3}} \:+\:\mathrm{3}{x} \\ $$$${f}\:^{−\mathrm{1}} \left({x}\right)\:\:=\:\:? \\ $$
Answered by mr W last updated on 20/Mar/20

$${y}={x}^{\mathrm{3}} +\mathrm{3}{x} \\ $$$${x}^{\mathrm{3}} +\mathrm{3}{x}−{y}=\mathrm{0} \\ $$$$\Rightarrow{x}=\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{1}+\frac{{y}^{\mathrm{2}} }{\mathrm{4}}}+\frac{{y}}{\mathrm{2}}}−\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{1}+\frac{{y}^{\mathrm{2}} }{\mathrm{4}}}−\frac{{y}}{\mathrm{2}}} \\ $$$$\Rightarrow{f}^{−\mathrm{1}} \left({x}\right)=\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{4}}}+\frac{{x}}{\mathrm{2}}}−\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{4}}}−\frac{{x}}{\mathrm{2}}} \\ $$
Commented by jagoll last updated on 20/Mar/20

$$\mathrm{cardano}? \\ $$
Commented by mr W last updated on 20/Mar/20

$${yes} \\ $$
