Menu Close

f-x-x-6-100x-5-100x-4-100x-3-100x-2-100x-100-f-99-

Tinku Tara 0 Comments
Pin




Question Number 175959 by BaliramKumar last updated on 10/Sep/22
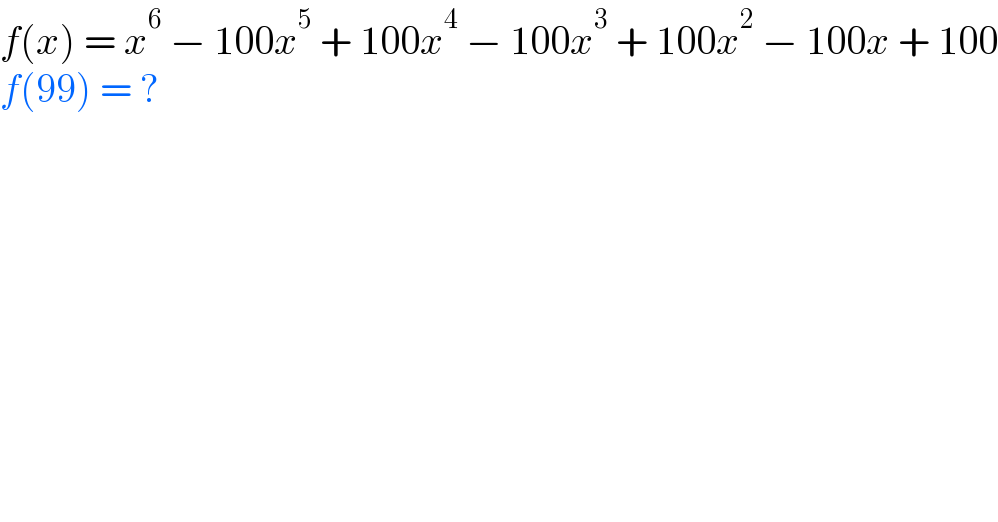
f(x) = x^6 − 100x^5 + 100x^4 − 100x^3 + 100x^2 − 100x + 100 f(99) = ?
$${f}\left({x}\right)\:=\:{x}^{\mathrm{6}} \:−\:\mathrm{100}{x}^{\mathrm{5}} \:+\:\mathrm{100}{x}^{\mathrm{4}} \:−\:\mathrm{100}{x}^{\mathrm{3}} \:+\:\mathrm{100}{x}^{\mathrm{2}} \:−\:\mathrm{100}{x}\:+\:\mathrm{100} \\ $$$${f}\left(\mathrm{99}\right)\:=\:? \\ $$
Commented by infinityaction last updated on 10/Sep/22
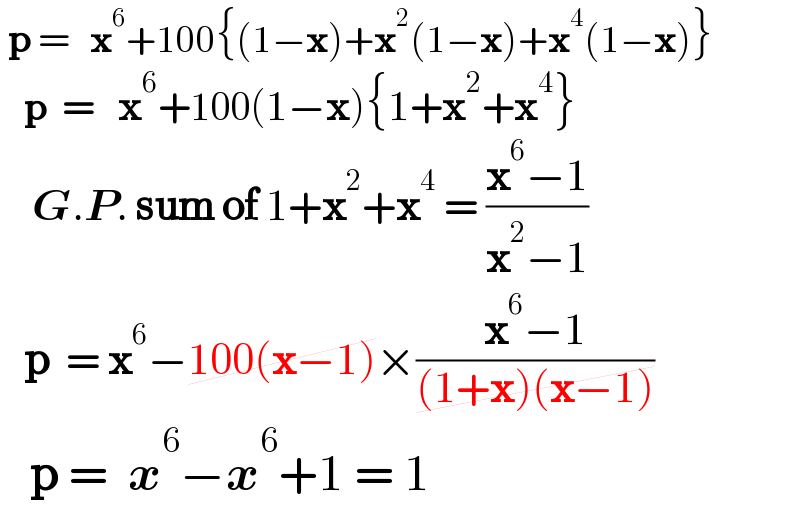
p = x^6 +100{(1−x)+x^2 (1−x)+x^4 (1−x)} p = x^6 +100(1−x){1+x^2 +x^4 } G.P. sum of 1+x^2 +x^4 = ((x^6 −1)/(x^2 −1)) p = x^6 −100(x−1)×((x^6 −1)/((1+x)(x−1))) p = x^6 −x^6 +1 = 1
$$\:\boldsymbol{\mathrm{p}}\:=\:\:\:\boldsymbol{\mathrm{x}}^{\mathrm{6}} +\mathrm{100}\left\{\left(\mathrm{1}−\boldsymbol{\mathrm{x}}\right)+\boldsymbol{\mathrm{x}}^{\mathrm{2}} \left(\mathrm{1}−\boldsymbol{\mathrm{x}}\right)+\boldsymbol{\mathrm{x}}^{\mathrm{4}} \left(\mathrm{1}−\boldsymbol{\mathrm{x}}\right)\right\} \\ $$$$\:\:\:\boldsymbol{\mathrm{p}}\:\:=\:\:\:\boldsymbol{\mathrm{x}}^{\mathrm{6}} +\mathrm{100}\left(\mathrm{1}−\boldsymbol{\mathrm{x}}\right)\left\{\mathrm{1}+\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{x}}^{\mathrm{4}} \right\} \\ $$$$\:\:\:\:\boldsymbol{{G}}.\boldsymbol{{P}}.\:\boldsymbol{\mathrm{sum}}\:\boldsymbol{\mathrm{of}}\:\mathrm{1}+\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{x}}^{\mathrm{4}} \:=\:\frac{\boldsymbol{\mathrm{x}}^{\mathrm{6}} −\mathrm{1}}{\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\:\:\:\boldsymbol{\mathrm{p}}\:\:=\:\boldsymbol{\mathrm{x}}^{\mathrm{6}} −\cancel{\mathrm{100}\left(\boldsymbol{\mathrm{x}}−\mathrm{1}\right)}×\frac{\boldsymbol{\mathrm{x}}^{\mathrm{6}} −\mathrm{1}}{\cancel{\left(\mathrm{1}+\boldsymbol{\mathrm{x}}\right)\left(\boldsymbol{\mathrm{x}}−\mathrm{1}\right)}} \\ $$$$\:\:\:\boldsymbol{\mathrm{p}}\:=\:\:\boldsymbol{{x}}^{\mathrm{6}} −\boldsymbol{{x}}^{\mathrm{6}} +\mathrm{1}\:=\:\mathrm{1} \\ $$
Commented by BaliramKumar last updated on 10/Sep/22
thanks sir
$${thanks}\:\:\:{sir} \\ $$
Answered by Rasheed.Sindhi last updated on 10/Sep/22
f(x) = x^6 − 100x^5 + 100x^4 − 100x^3 + 100x^2 − 100x + 100 =x^5 (x−100)+ 100x^4 − 100x^3 + 100x^2 − 100x + 100 f(99)=x^5 (99−100)+ 100x^4 − 100x^3 + 100x^2 − 100x + 100 =−x^5 + 100x^4 − 100x^3 + 100x^2 − 100x + 100 =x^4 (−x+100)− 100x^3 + 100x^2 − 100x + 100 =x^4 (−99+100)− 100x^3 + 100x^2 − 100x + 100 =x^4 − 100x^3 + 100x^2 − 100x + 100 =x^3 (x−100) + 100x^2 − 100x + 100 =x^3 (99−100) + 100x^2 − 100x + 100 =−x^3 + 100x^2 − 100x + 100 =x^2 (−x+100)− 100x + 100 =x^2 (−99+100)− 100x + 100 =x^2 − 100x + 100 =x(x− 100) + 100 =x(99− 100) + 100 =−x + 100 =−99 + 100 =1
$${f}\left({x}\right)\:=\:{x}^{\mathrm{6}} \:−\:\mathrm{100}{x}^{\mathrm{5}} \:+\:\mathrm{100}{x}^{\mathrm{4}} \:−\:\mathrm{100}{x}^{\mathrm{3}} \:+\:\mathrm{100}{x}^{\mathrm{2}} \:−\:\mathrm{100}{x}\:+\:\mathrm{100} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:={x}^{\mathrm{5}} \left({x}−\mathrm{100}\right)+\:\mathrm{100}{x}^{\mathrm{4}} \:−\:\mathrm{100}{x}^{\mathrm{3}} \:+\:\mathrm{100}{x}^{\mathrm{2}} \:−\:\mathrm{100}{x}\:+\:\mathrm{100} \\ $$$${f}\left(\mathrm{99}\right)={x}^{\mathrm{5}} \left(\mathrm{99}−\mathrm{100}\right)+\:\mathrm{100}{x}^{\mathrm{4}} \:−\:\mathrm{100}{x}^{\mathrm{3}} \:+\:\mathrm{100}{x}^{\mathrm{2}} \:−\:\mathrm{100}{x}\:+\:\mathrm{100} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=−{x}^{\mathrm{5}} +\:\mathrm{100}{x}^{\mathrm{4}} \:−\:\mathrm{100}{x}^{\mathrm{3}} \:+\:\mathrm{100}{x}^{\mathrm{2}} \:−\:\mathrm{100}{x}\:+\:\mathrm{100} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:={x}^{\mathrm{4}} \left(−{x}+\mathrm{100}\right)−\:\mathrm{100}{x}^{\mathrm{3}} \:+\:\mathrm{100}{x}^{\mathrm{2}} \:−\:\mathrm{100}{x}\:+\:\mathrm{100} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:={x}^{\mathrm{4}} \left(−\mathrm{99}+\mathrm{100}\right)−\:\mathrm{100}{x}^{\mathrm{3}} \:+\:\mathrm{100}{x}^{\mathrm{2}} \:−\:\mathrm{100}{x}\:+\:\mathrm{100} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:={x}^{\mathrm{4}} −\:\mathrm{100}{x}^{\mathrm{3}} \:+\:\mathrm{100}{x}^{\mathrm{2}} \:−\:\mathrm{100}{x}\:+\:\mathrm{100} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:={x}^{\mathrm{3}} \left({x}−\mathrm{100}\right)\:+\:\mathrm{100}{x}^{\mathrm{2}} \:−\:\mathrm{100}{x}\:+\:\mathrm{100} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:={x}^{\mathrm{3}} \left(\mathrm{99}−\mathrm{100}\right)\:+\:\mathrm{100}{x}^{\mathrm{2}} \:−\:\mathrm{100}{x}\:+\:\mathrm{100} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=−{x}^{\mathrm{3}} \:+\:\mathrm{100}{x}^{\mathrm{2}} \:−\:\mathrm{100}{x}\:+\:\mathrm{100} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:={x}^{\mathrm{2}} \left(−{x}+\mathrm{100}\right)−\:\mathrm{100}{x}\:+\:\mathrm{100} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:={x}^{\mathrm{2}} \left(−\mathrm{99}+\mathrm{100}\right)−\:\mathrm{100}{x}\:+\:\mathrm{100} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:={x}^{\mathrm{2}} −\:\mathrm{100}{x}\:+\:\mathrm{100} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:={x}\left({x}−\:\mathrm{100}\right)\:+\:\mathrm{100} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:={x}\left(\mathrm{99}−\:\mathrm{100}\right)\:+\:\mathrm{100} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=−{x}\:+\:\mathrm{100} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=−\mathrm{99}\:+\:\mathrm{100} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1} \\ $$
Commented by BaliramKumar last updated on 10/Sep/22
thanks sir
$$\mathrm{thanks}\:\:\mathrm{sir} \\ $$
Answered by Rasheed.Sindhi last updated on 10/Sep/22
f(99)=Remainder of f(x)/(x−99) By Synthetic Division: determinant (((99)),1,(-100),(100),(-100),(100),(-100),(100)),(,,( +99),(-99),( +99),(-99),( 99),(-99)),(,1,( -1),( 1),( -1),( 1),( -1),( determinant ((1))^ ))) f(99)=1
$${f}\left(\mathrm{99}\right)={Remainder}\:{of}\:\:\:{f}\left({x}\right)/\left({x}−\mathrm{99}\right) \\ $$$$\mathcal{B}{y}\:\mathcal{S}{ynthetic}\:\mathcal{D}{ivision}: \\ $$$$\:\begin{array}{|c|c|c|}{\left.\mathrm{99}\right)}&\hline{\mathrm{1}}&\hline{-\mathrm{100}}&\hline{\mathrm{100}}&\hline{-\mathrm{100}}&\hline{\mathrm{100}}&\hline{-\mathrm{100}}&\hline{\mathrm{100}}\\{}&\hline{}&\hline{\:+\mathrm{99}}&\hline{-\mathrm{99}}&\hline{\:+\mathrm{99}}&\hline{-\mathrm{99}}&\hline{\:\:\:\:\:\mathrm{99}}&\hline{-\mathrm{99}}\\{}&\hline{\mathrm{1}}&\hline{\:\:\:\:\:-\mathrm{1}}&\hline{\:\:\:\:\:\mathrm{1}}&\hline{\:\:\:\:-\mathrm{1}}&\hline{\:\:\:\:\:\mathrm{1}}&\hline{\:\:\:\:\:-\mathrm{1}}&\hline{\:\begin{array}{|c|}{\mathrm{1}}\\\hline\end{array}^{} }\\\hline\end{array} \\ $$$${f}\left(\mathrm{99}\right)=\mathrm{1}\: \\ $$
Commented by Tawa11 last updated on 15/Sep/22
Great sirs.
$$\mathrm{Great}\:\mathrm{sirs}. \\ $$
Answered by Devendra291999 last updated on 10/Sep/22
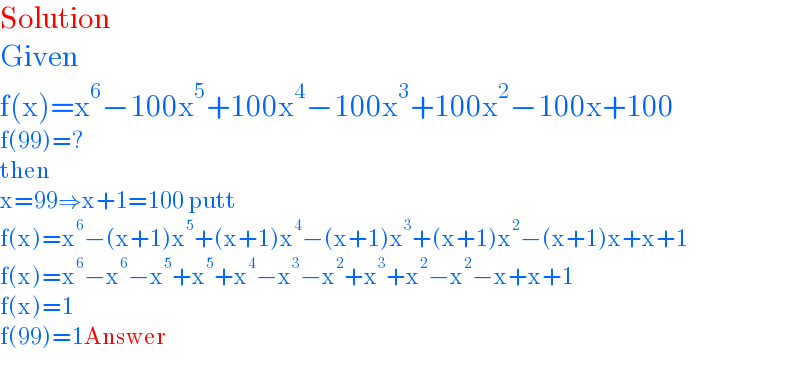
Solution Given f(x)=x^6 −100x^5 +100x^4 −100x^3 +100x^2 −100x+100 f(99)=? then x=99⇒x+1=100 putt f(x)=x^6 −(x+1)x^5 +(x+1)x^4 −(x+1)x^3 +(x+1)x^2 −(x+1)x+x+1 f(x)=x^6 −x^6 −x^5 +x^5 +x^4 −x^3 −x^2 +x^3 +x^2 −x^2 −x+x+1 f(x)=1 f(99)=1Answer
$$\mathrm{Solution} \\ $$$$\mathrm{Given} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{6}} −\mathrm{100x}^{\mathrm{5}} +\mathrm{100x}^{\mathrm{4}} −\mathrm{100x}^{\mathrm{3}} +\mathrm{100x}^{\mathrm{2}} −\mathrm{100x}+\mathrm{100} \\ $$$$\mathrm{f}\left(\mathrm{99}\right)=? \\ $$$$\mathrm{then} \\ $$$$\mathrm{x}=\mathrm{99}\Rightarrow\mathrm{x}+\mathrm{1}=\mathrm{100}\:\mathrm{putt} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{6}} −\left(\mathrm{x}+\mathrm{1}\right)\mathrm{x}^{\mathrm{5}} +\left(\mathrm{x}+\mathrm{1}\right)\mathrm{x}^{\mathrm{4}} −\left(\mathrm{x}+\mathrm{1}\right)\mathrm{x}^{\mathrm{3}} +\left(\mathrm{x}+\mathrm{1}\right)\mathrm{x}^{\mathrm{2}} −\left(\mathrm{x}+\mathrm{1}\right)\mathrm{x}+\mathrm{x}+\mathrm{1} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{6}} −\mathrm{x}^{\mathrm{6}} −\mathrm{x}^{\mathrm{5}} +\mathrm{x}^{\mathrm{5}} +\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{3}} −\mathrm{x}^{\mathrm{2}} +\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{x}+\mathrm{1} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{1} \\ $$$$\mathrm{f}\left(\mathrm{99}\right)=\mathrm{1Answer} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *