Question Number 165552 by mnjuly1970 last updated on 03/Feb/22
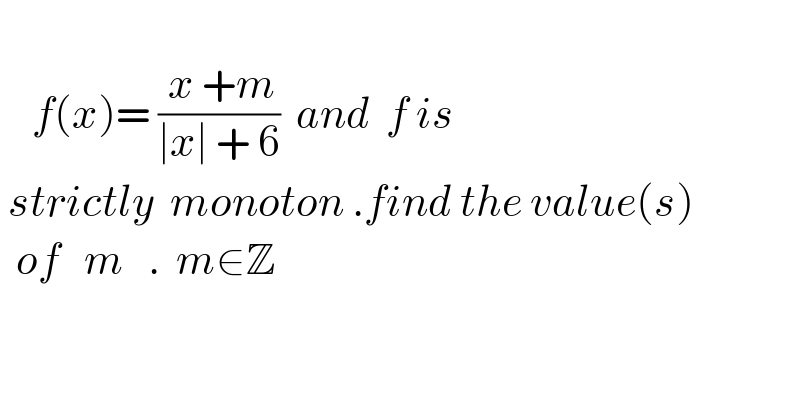
$$ \\ $$$$\:\:\:\:{f}\left({x}\right)=\:\frac{\:{x}\:+{m}}{\mid{x}\mid\:+\:\mathrm{6}}\:\:{and}\:\:{f}\:{is} \\ $$$$\:{strictly}\:\:{monoton}\:.{find}\:{the}\:{value}\left({s}\right) \\ $$$$\:\:{of}\:\:\:{m}\:\:\:.\:\:{m}\in\mathbb{Z} \\ $$
Answered by TheSupreme last updated on 03/Feb/22
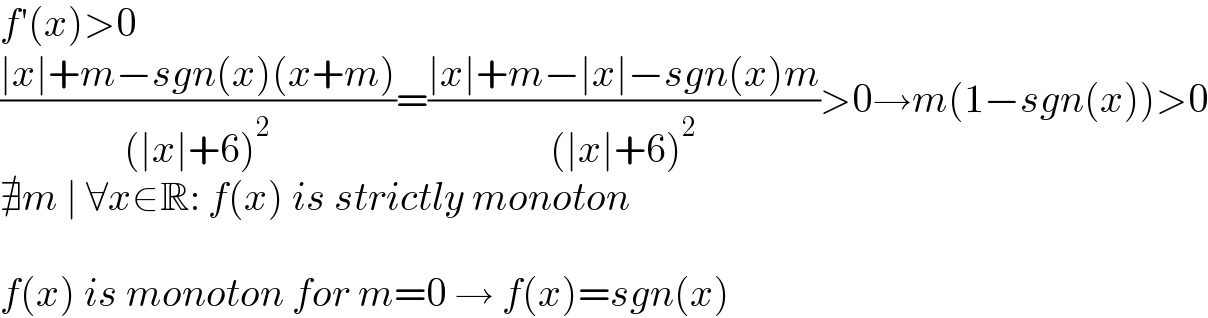
$${f}'\left({x}\right)>\mathrm{0} \\ $$$$\frac{\mid{x}\mid+{m}−{sgn}\left({x}\right)\left({x}+{m}\right)}{\left(\mid{x}\mid+\mathrm{6}\right)^{\mathrm{2}} }=\frac{\mid{x}\mid+{m}−\mid{x}\mid−{sgn}\left({x}\right){m}}{\left(\mid{x}\mid+\mathrm{6}\right)^{\mathrm{2}} }>\mathrm{0}\rightarrow{m}\left(\mathrm{1}−{sgn}\left({x}\right)\right)>\mathrm{0} \\ $$$$\nexists{m}\:\mid\:\forall{x}\in\mathbb{R}:\:{f}\left({x}\right)\:{is}\:{strictly}\:{monoton} \\ $$$$ \\ $$$${f}\left({x}\right)\:{is}\:{monoton}\:{for}\:{m}=\mathrm{0}\:\rightarrow\:{f}\left({x}\right)={sgn}\left({x}\right) \\ $$
Answered by mahdipoor last updated on 03/Feb/22
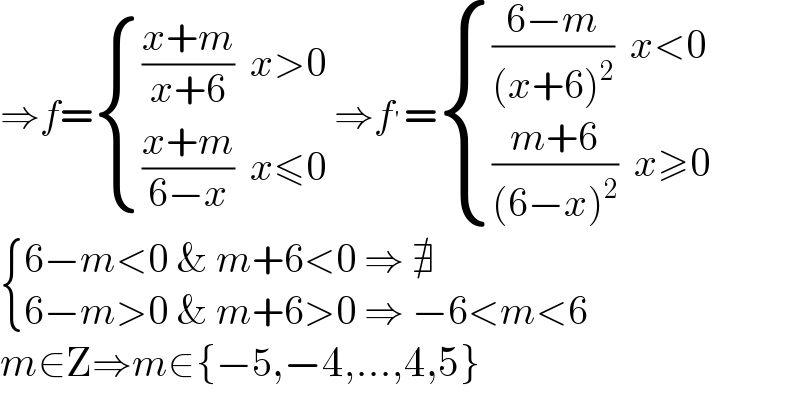
$$\Rightarrow{f}=\begin{cases}{\frac{{x}+{m}}{{x}+\mathrm{6}}\:\:{x}>\mathrm{0}}\\{\frac{{x}+{m}}{\mathrm{6}−{x}}\:\:{x}\leqslant\mathrm{0}}\end{cases}\:\Rightarrow{f}^{'} =\begin{cases}{\frac{\mathrm{6}−{m}}{\left({x}+\mathrm{6}\right)^{\mathrm{2}} }\:\:{x}<\mathrm{0}}\\{\frac{{m}+\mathrm{6}}{\left(\mathrm{6}−{x}\right)^{\mathrm{2}} }\:\:{x}\geqslant\mathrm{0}}\end{cases} \\ $$$$\begin{cases}{\mathrm{6}−{m}<\mathrm{0}\:\&\:{m}+\mathrm{6}<\mathrm{0}\:\Rightarrow\:\nexists}\\{\mathrm{6}−{m}>\mathrm{0}\:\&\:{m}+\mathrm{6}>\mathrm{0}\:\Rightarrow\:−\mathrm{6}<{m}<\mathrm{6}}\end{cases} \\ $$$${m}\in\mathrm{Z}\Rightarrow{m}\in\left\{−\mathrm{5},−\mathrm{4},…,\mathrm{4},\mathrm{5}\right\} \\ $$
