Menu Close

f-x-x-x-1-f-1-

Tinku Tara 0 Comments
Pin




Question Number 122393 by benjo_mathlover last updated on 16/Nov/20
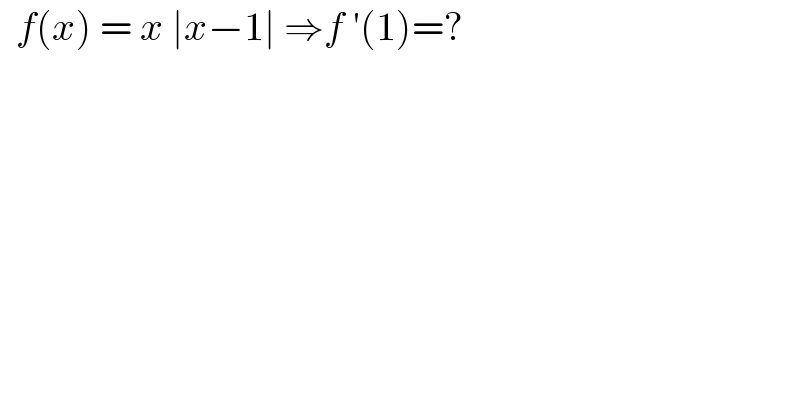
f(x) = x ∣x−1∣ ⇒f ′(1)=?
f(x)=x∣x−1∣⇒f′(1)=?
Answered by MJS_new last updated on 16/Nov/20
does not exist
doesnotexist
Answered by Bird last updated on 17/Nov/20
lim_(h→0^+ ) ((f(1+h)−f(1))/h) =lim_(h→o^+ ) (((1+h)h)/h) =lim_(h→0^+ ) 1+h=1 lim_(h→0^− ) ((f(1+h)−f(1))/h) =lim_(h→0^− ) (((1+h)(−h))/h)=lim_(h→0^− ) −(1+h) =−1 its clear thst f is not derivable at 1 ⇒f^′ (1) dont exist
limh→0+f(1+h)−f(1)h=limh→o+(1+h)hh=limh→0+1+h=1limh→0−f(1+h)−f(1)h=limh→0−(1+h)(−h)h=limh→0−−(1+h)=−1itsclearthstfisnotderivableat1⇒f′(1)dontexist

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *