Question Number 184942 by mnjuly1970 last updated on 14/Jan/23
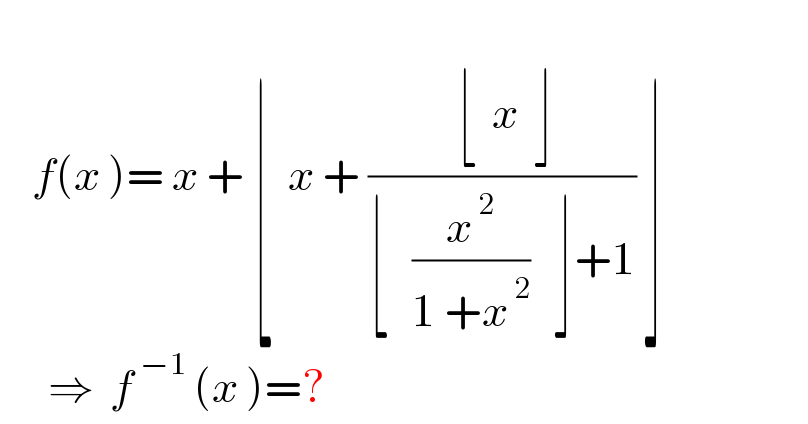
$$ \\ $$$$\:\:\:\:{f}\left({x}\:\right)=\:{x}\:+\:\lfloor\:\:{x}\:+\:\frac{\:\lfloor\:\:\underset{} {\overset{} {{x}}}\:\:\rfloor}{\lfloor\:\:\:\frac{{x}^{\:\mathrm{2}} }{\mathrm{1}\:+{x}^{\:\mathrm{2}} }\:\:\:\rfloor+\mathrm{1}}\:\rfloor \\ $$$$\:\:\:\:\:\:\Rightarrow\:\:{f}^{\:−\mathrm{1}} \:\left({x}\:\right)=? \\ $$
Commented by Frix last updated on 14/Jan/23
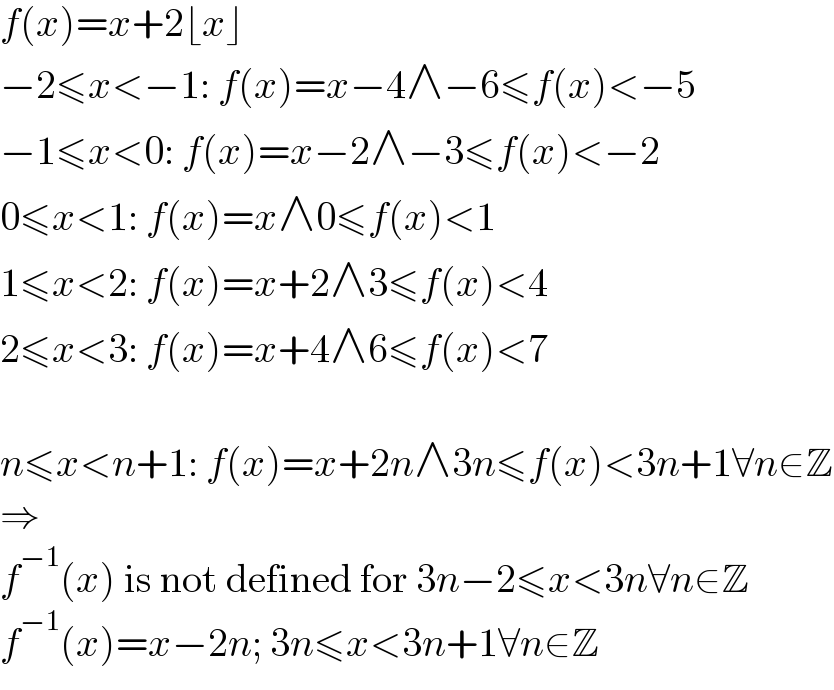
$${f}\left({x}\right)={x}+\mathrm{2}\lfloor{x}\rfloor \\ $$$$−\mathrm{2}\leqslant{x}<−\mathrm{1}:\:{f}\left({x}\right)={x}−\mathrm{4}\wedge−\mathrm{6}\leqslant{f}\left({x}\right)<−\mathrm{5} \\ $$$$−\mathrm{1}\leqslant{x}<\mathrm{0}:\:{f}\left({x}\right)={x}−\mathrm{2}\wedge−\mathrm{3}\leqslant{f}\left({x}\right)<−\mathrm{2} \\ $$$$\mathrm{0}\leqslant{x}<\mathrm{1}:\:{f}\left({x}\right)={x}\wedge\mathrm{0}\leqslant{f}\left({x}\right)<\mathrm{1} \\ $$$$\mathrm{1}\leqslant{x}<\mathrm{2}:\:{f}\left({x}\right)={x}+\mathrm{2}\wedge\mathrm{3}\leqslant{f}\left({x}\right)<\mathrm{4} \\ $$$$\mathrm{2}\leqslant{x}<\mathrm{3}:\:{f}\left({x}\right)={x}+\mathrm{4}\wedge\mathrm{6}\leqslant{f}\left({x}\right)<\mathrm{7} \\ $$$$ \\ $$$${n}\leqslant{x}<{n}+\mathrm{1}:\:{f}\left({x}\right)={x}+\mathrm{2}{n}\wedge\mathrm{3}{n}\leqslant{f}\left({x}\right)<\mathrm{3}{n}+\mathrm{1}\forall{n}\in\mathbb{Z} \\ $$$$\Rightarrow \\ $$$${f}^{−\mathrm{1}} \left({x}\right)\:\mathrm{is}\:\mathrm{not}\:\mathrm{defined}\:\mathrm{for}\:\mathrm{3}{n}−\mathrm{2}\leqslant{x}<\mathrm{3}{n}\forall{n}\in\mathbb{Z} \\ $$$${f}^{−\mathrm{1}} \left({x}\right)={x}−\mathrm{2}{n};\:\mathrm{3}{n}\leqslant{x}<\mathrm{3}{n}+\mathrm{1}\forall{n}\in\mathbb{Z} \\ $$
Commented by mnjuly1970 last updated on 14/Jan/23
$${mercey}\:{sir}\:{frix} \\ $$
