Question Number 98398 by bemath last updated on 13/Jun/20
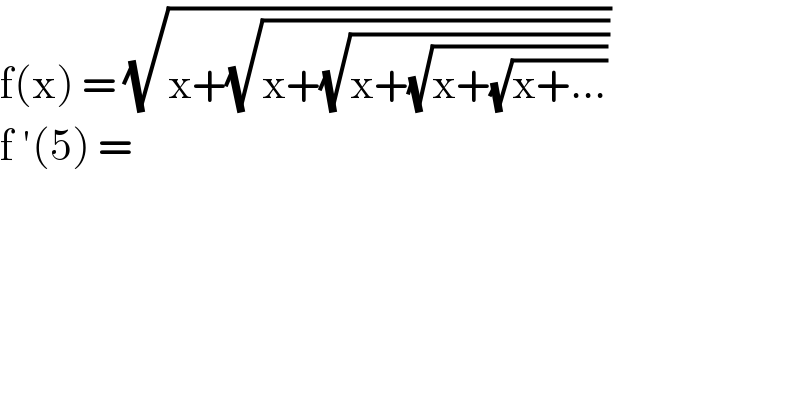
$$\mathrm{f}\left(\mathrm{x}\right)\:=\:\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+…}}}}} \\ $$$$\mathrm{f}\:'\left(\mathrm{5}\right)\:=\: \\ $$
Commented by bobhans last updated on 14/Jun/20
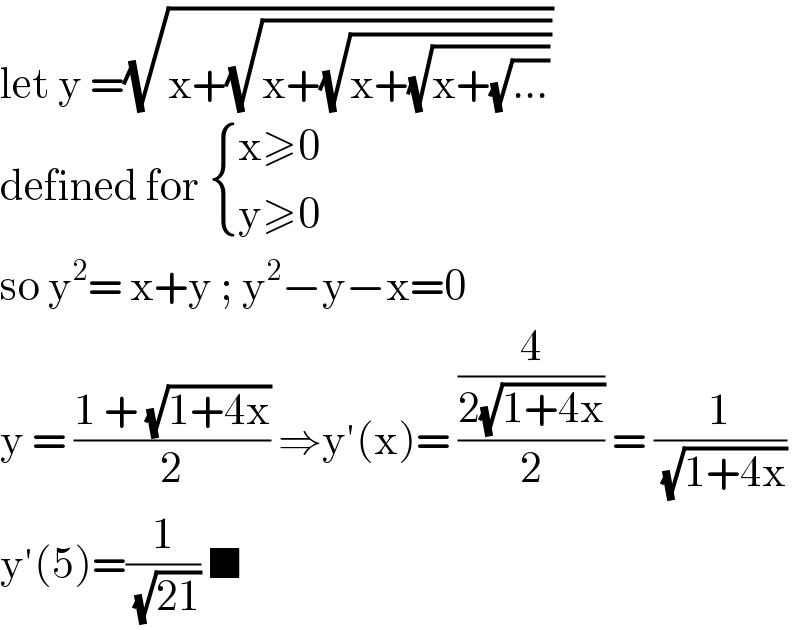
$$\mathrm{let}\:\mathrm{y}\:=\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{…}}}}} \\ $$$$\mathrm{defined}\:\mathrm{for}\:\begin{cases}{\mathrm{x}\geqslant\mathrm{0}}\\{\mathrm{y}\geqslant\mathrm{0}}\end{cases} \\ $$$$\mathrm{so}\:\mathrm{y}^{\mathrm{2}} =\:\mathrm{x}+\mathrm{y}\:;\:\mathrm{y}^{\mathrm{2}} −\mathrm{y}−\mathrm{x}=\mathrm{0} \\ $$$$\mathrm{y}\:=\:\frac{\mathrm{1}\:+\:\sqrt{\mathrm{1}+\mathrm{4x}}}{\mathrm{2}}\:\Rightarrow\mathrm{y}'\left(\mathrm{x}\right)=\:\frac{\frac{\mathrm{4}}{\mathrm{2}\sqrt{\mathrm{1}+\mathrm{4x}}}}{\mathrm{2}}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4x}}} \\ $$$$\mathrm{y}'\left(\mathrm{5}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{21}}}\:\blacksquare \\ $$
Commented by mr W last updated on 14/Jun/20

$${absolutely}\:{correct}\:{sir}! \\ $$$${even}\:{without}\:{knowledge}\:{about}\:{calculus} \\ $$$${it}'{s}\:{easy}\:{to}\:{see}: \\ $$$${y}\left(\mathrm{5}\right)=\sqrt{\mathrm{5}+\sqrt{\mathrm{5}+\sqrt{\mathrm{5}+\sqrt{…}}}}>\sqrt{\mathrm{5}}>\mathrm{0} \\ $$$${y}\left(\mathrm{6}\right)=\sqrt{\mathrm{6}+\sqrt{\mathrm{6}+\sqrt{\mathrm{6}+\sqrt{…}}}}>\sqrt{\mathrm{5}+\sqrt{\mathrm{5}+\sqrt{\mathrm{5}+\sqrt{…}}}} \\ $$$$\frac{{y}\left(\mathrm{6}\right)−{y}\left(\mathrm{5}\right)}{\mathrm{6}−\mathrm{5}}>\mathrm{0}\:\Rightarrow{y}'\left(\mathrm{5}\right)>\mathrm{0} \\ $$
Answered by smridha last updated on 13/Jun/20
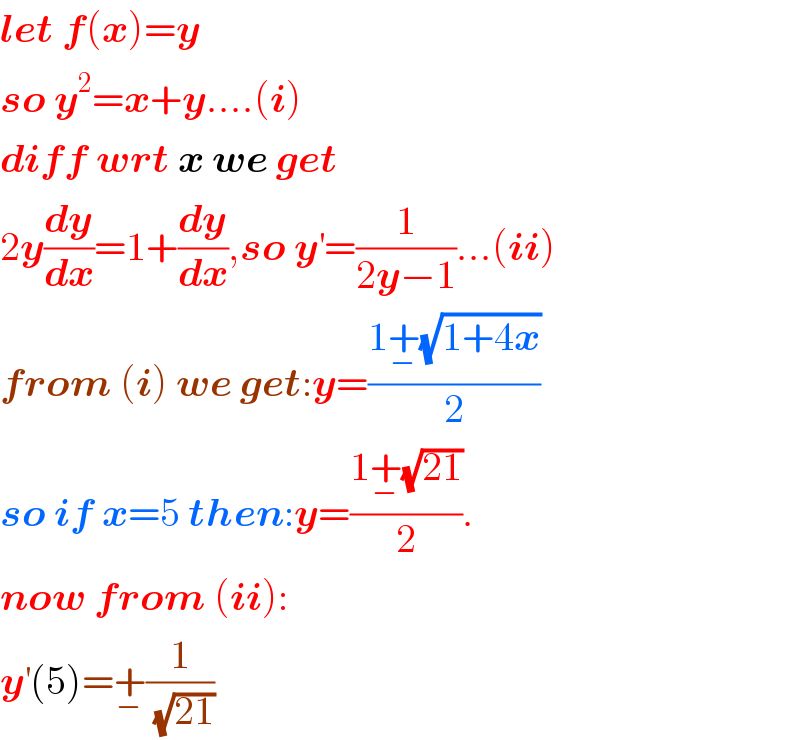
$$\boldsymbol{{let}}\:\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)=\boldsymbol{{y}} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{y}}^{\mathrm{2}} =\boldsymbol{{x}}+\boldsymbol{{y}}….\left(\boldsymbol{{i}}\right) \\ $$$$\boldsymbol{{diff}}\:\boldsymbol{{wrt}}\:\boldsymbol{{x}}\:\boldsymbol{{we}}\:\boldsymbol{{get}} \\ $$$$\mathrm{2}\boldsymbol{{y}}\frac{\boldsymbol{{dy}}}{\boldsymbol{{dx}}}=\mathrm{1}+\frac{\boldsymbol{{dy}}}{\boldsymbol{{dx}}},\boldsymbol{{so}}\:\boldsymbol{{y}}^{'} =\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{{y}}−\mathrm{1}}…\left(\boldsymbol{{ii}}\right) \\ $$$$\boldsymbol{{from}}\:\left(\boldsymbol{{i}}\right)\:\boldsymbol{{we}}\:\boldsymbol{{get}}:\boldsymbol{{y}}=\frac{\mathrm{1}\underset{−} {+}\sqrt{\mathrm{1}+\mathrm{4}\boldsymbol{{x}}}}{\mathrm{2}} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{if}}\:\boldsymbol{{x}}=\mathrm{5}\:\boldsymbol{{then}}:\boldsymbol{{y}}=\frac{\mathrm{1}\underset{−} {+}\sqrt{\mathrm{21}}}{\mathrm{2}}. \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{from}}\:\left(\boldsymbol{{ii}}\right): \\ $$$$\boldsymbol{{y}}^{'} \left(\mathrm{5}\right)=\underset{−} {+}\frac{\mathrm{1}}{\:\sqrt{\mathrm{21}}} \\ $$
Commented by bemath last updated on 13/Jun/20

$$\mathrm{yeahhh}… \\ $$
Answered by abdomathmax last updated on 13/Jun/20
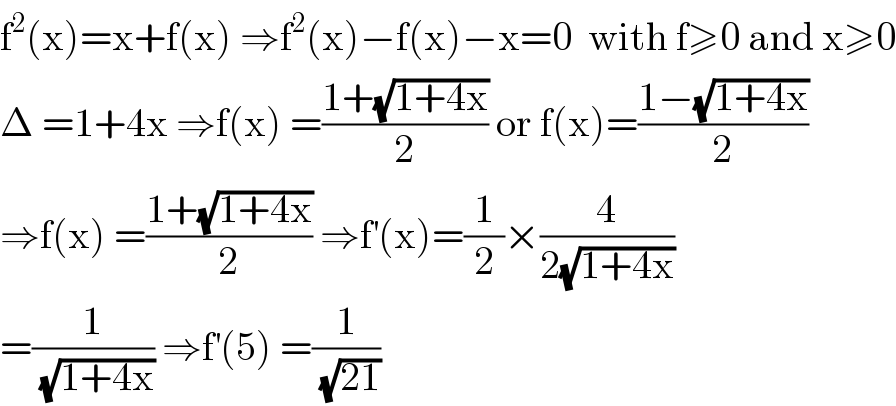
$$\mathrm{f}^{\mathrm{2}} \left(\mathrm{x}\right)=\mathrm{x}+\mathrm{f}\left(\mathrm{x}\right)\:\Rightarrow\mathrm{f}^{\mathrm{2}} \left(\mathrm{x}\right)−\mathrm{f}\left(\mathrm{x}\right)−\mathrm{x}=\mathrm{0}\:\:\mathrm{with}\:\mathrm{f}\geqslant\mathrm{0}\:\mathrm{and}\:\mathrm{x}\geqslant\mathrm{0} \\ $$$$\Delta\:=\mathrm{1}+\mathrm{4x}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4x}}}{\mathrm{2}}\:\mathrm{or}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}−\sqrt{\mathrm{1}+\mathrm{4x}}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4x}}}{\mathrm{2}}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{4}}{\mathrm{2}\sqrt{\mathrm{1}+\mathrm{4x}}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4x}}}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{5}\right)\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{21}}} \\ $$
Commented by mr W last updated on 13/Jun/20
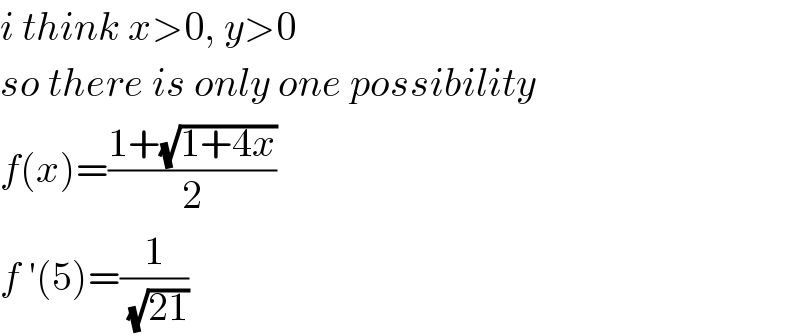
$${i}\:{think}\:{x}>\mathrm{0},\:{y}>\mathrm{0} \\ $$$${so}\:{there}\:{is}\:{only}\:{one}\:{possibility} \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4}{x}}}{\mathrm{2}} \\ $$$${f}\:'\left(\mathrm{5}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{21}}} \\ $$
Commented by mathmax by abdo last updated on 13/Jun/20
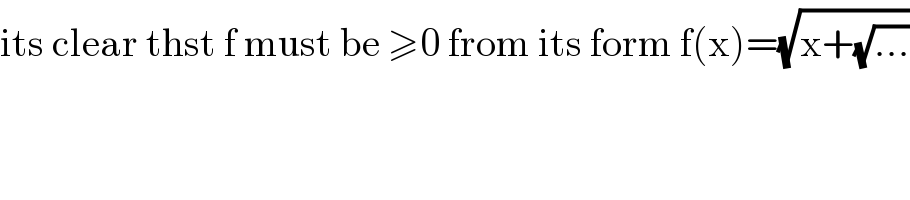
$$\mathrm{its}\:\mathrm{clear}\:\mathrm{thst}\:\mathrm{f}\:\mathrm{must}\:\mathrm{be}\:\geqslant\mathrm{0}\:\mathrm{from}\:\mathrm{its}\:\mathrm{form}\:\mathrm{f}\left(\mathrm{x}\right)=\sqrt{\mathrm{x}+\sqrt{…}} \\ $$
Answered by smridha last updated on 13/Jun/20
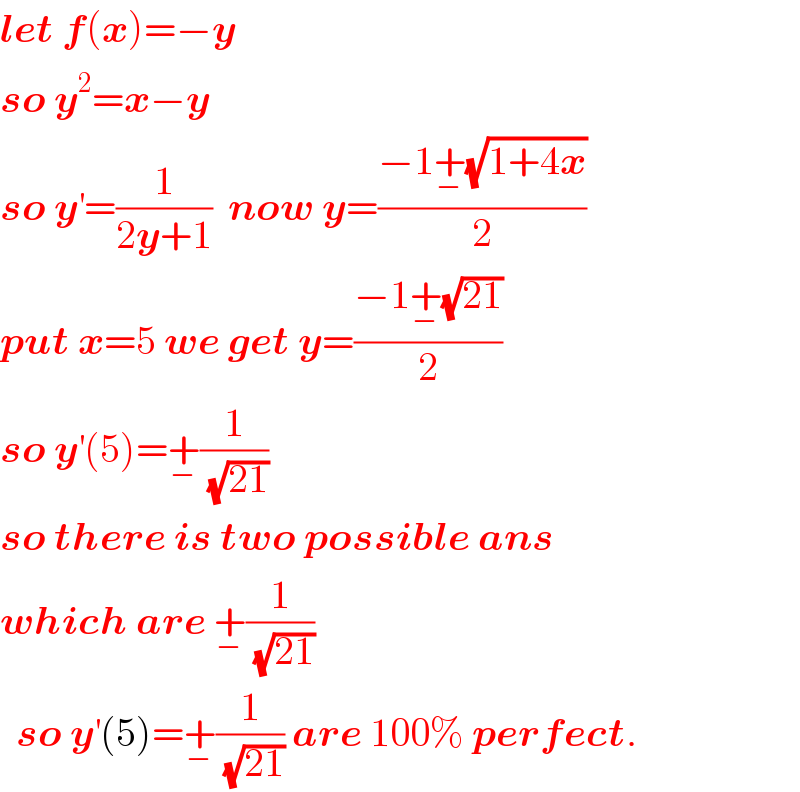
$$\boldsymbol{{let}}\:\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)=−\boldsymbol{{y}} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{y}}^{\mathrm{2}} =\boldsymbol{{x}}−\boldsymbol{{y}} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{y}}^{'} =\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{{y}}+\mathrm{1}}\:\:\boldsymbol{{now}}\:\boldsymbol{{y}}=\frac{−\mathrm{1}\underset{−} {+}\sqrt{\mathrm{1}+\mathrm{4}\boldsymbol{{x}}}}{\mathrm{2}} \\ $$$$\boldsymbol{{put}}\:\boldsymbol{{x}}=\mathrm{5}\:\boldsymbol{{we}}\:\boldsymbol{{get}}\:\boldsymbol{{y}}=\frac{−\mathrm{1}\underset{−} {+}\sqrt{\mathrm{21}}}{\mathrm{2}} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{y}}^{'} \left(\mathrm{5}\right)=\underset{−} {+}\frac{\mathrm{1}}{\:\sqrt{\mathrm{21}}} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{there}}\:\boldsymbol{{is}}\:\boldsymbol{{two}}\:\boldsymbol{{possible}}\:\boldsymbol{{ans}} \\ $$$$\boldsymbol{{which}}\:\boldsymbol{{are}}\:\underset{−} {+}\frac{\mathrm{1}}{\:\sqrt{\mathrm{21}}} \\ $$$$\:\:\boldsymbol{{so}}\:\boldsymbol{{y}}^{'} \left(\mathrm{5}\right)=\underset{−} {+}\frac{\mathrm{1}}{\:\sqrt{\mathrm{21}}}\:\boldsymbol{{are}}\:\mathrm{100\%}\:\boldsymbol{{perfect}}. \\ $$
Answered by smridha last updated on 14/Jun/20

$$\boldsymbol{{ohh}}\:\boldsymbol{{then}}\:\boldsymbol{{if}}\:\boldsymbol{{x}}^{\mathrm{2}} =\mathrm{4}\:\boldsymbol{{then}}\: \\ $$$$\boldsymbol{{x}}=\sqrt{\mathrm{4}}\:\boldsymbol{{and}}\:\boldsymbol{{x}}\:\boldsymbol{{has}}\:\boldsymbol{{only}}\:\boldsymbol{{one}}\:\boldsymbol{{value}} \\ $$$$\boldsymbol{{t}}{ha}\boldsymbol{{t}}\:\boldsymbol{{is}}+\:\mathrm{2}\:\boldsymbol{{wow}}\:\boldsymbol{{that}}\:\boldsymbol{{great}}\:\boldsymbol{{very}}\:\boldsymbol{{funny}} \\ $$$$\boldsymbol{{what}}\:\boldsymbol{{is}}\:\boldsymbol{{the}}\:\boldsymbol{{meaning}}\:\boldsymbol{{of}}\:\boldsymbol{{square}} \\ $$$$\boldsymbol{{root}}…\boldsymbol{{I}}\:\boldsymbol{{think}}\:\boldsymbol{{it}}\:\boldsymbol{{is}}\:\boldsymbol{{new}}\:\boldsymbol{{invension}} \\ $$$$\boldsymbol{{that}}\:^{\mathrm{2}} \sqrt{\:\:}\:\:\:\boldsymbol{{means}}\:\boldsymbol{{only}}\:+. \\ $$$$\boldsymbol{{x}}\:\boldsymbol{{is}}\:\boldsymbol{{under}}\:\boldsymbol{{square}}\:\boldsymbol{{root}}\:\boldsymbol{{so}}\:\boldsymbol{{we}} \\ $$$$\boldsymbol{{cannot}}\:\boldsymbol{{considered}}\:\boldsymbol{{only}}\:\boldsymbol{{possitive}} \\ $$$$\boldsymbol{{value}}…\boldsymbol{{it}}\:\boldsymbol{{is}}\:\boldsymbol{{very}}\:\boldsymbol{{childish}}\:\boldsymbol{{comment}} \\ $$$$\boldsymbol{{i}}\:\boldsymbol{{ever}}\:\boldsymbol{{read}}… \\ $$$$\boldsymbol{{at}}\:\boldsymbol{{first}}\:\boldsymbol{{know}}\:\boldsymbol{{the}}\:\boldsymbol{{meaning}}\:\boldsymbol{{of}} \\ $$$$\boldsymbol{{square}}\:\boldsymbol{{root}}… \\ $$$$\sqrt{\mathrm{5}}\:>\mathrm{0}\:\boldsymbol{{when}}\:\boldsymbol{{we}}\:\boldsymbol{{consider}}\:\boldsymbol{{and}} \\ $$$$\boldsymbol{{take}}\:\boldsymbol{{the}}\:\boldsymbol{{possitive}}\:\boldsymbol{{value}} \\ $$$$\boldsymbol{{of}}\:\sqrt{\mathrm{5}}\:\boldsymbol{{not}}\:\boldsymbol{{the}}\:\boldsymbol{{negetive}}\:\boldsymbol{{value}} \\ $$$$\sqrt{\mathrm{5}}\approx\underset{−} {+}\mathrm{2}.\mathrm{236}\:{so}\:+\mathrm{2}.\mathrm{236}>\mathrm{0}\: \\ $$$$−\mathrm{2}.\mathrm{236}<\mathrm{0}. \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)=\underset{−} {+}\boldsymbol{{y}}\:\boldsymbol{{not}}\:\boldsymbol{{only}}\:+\boldsymbol{{y}}\:\boldsymbol{{or}}\:−\boldsymbol{{y}} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{the}}\:\boldsymbol{{genrel}}\:\boldsymbol{{silution}}\:\boldsymbol{{is}} \\ $$$$\boldsymbol{{y}}^{'} \left(\mathrm{5}\right)=\underset{−} {+}\frac{\mathrm{1}}{\:\sqrt{\mathrm{21}}}\:\boldsymbol{{always}}\:\boldsymbol{{be}}\:\boldsymbol{{perfect}}. \\ $$
Commented by bobhans last updated on 14/Jun/20
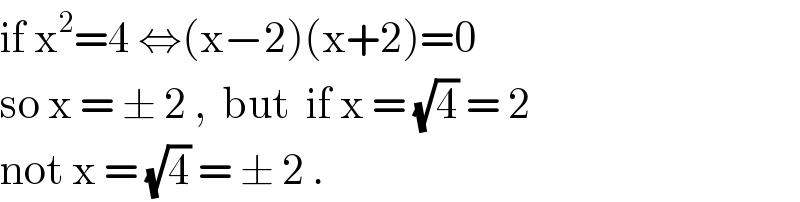
$$\mathrm{if}\:\mathrm{x}^{\mathrm{2}} =\mathrm{4}\:\Leftrightarrow\left(\mathrm{x}−\mathrm{2}\right)\left(\mathrm{x}+\mathrm{2}\right)=\mathrm{0} \\ $$$$\mathrm{so}\:\mathrm{x}\:=\:\pm\:\mathrm{2}\:,\:\:\mathrm{but}\:\:\mathrm{if}\:\mathrm{x}\:=\:\sqrt{\mathrm{4}}\:=\:\mathrm{2} \\ $$$$\mathrm{not}\:\mathrm{x}\:=\:\sqrt{\mathrm{4}}\:=\:\pm\:\mathrm{2}\:.\: \\ $$
Commented by smridha last updated on 14/Jun/20

$$\boldsymbol{{well}}\:\sqrt{\mathrm{4}}=\sqrt{\boldsymbol{{i}}^{\mathrm{4}} \mathrm{4}}=\boldsymbol{{i}}^{\mathrm{2}} .\mathrm{2}=−\mathrm{2}\:\boldsymbol{{it}}\:\boldsymbol{{is}}\:\boldsymbol{{also}} \\ $$$$\boldsymbol{{correct}}\:.\boldsymbol{{i}}^{\mathrm{4}} =\mathrm{1} \\ $$$$\boldsymbol{{so}}\:\sqrt{\boldsymbol{{i}}^{\mathrm{4}\boldsymbol{{n}}+\mathrm{4}} \boldsymbol{{x}}}=\boldsymbol{{i}}^{\mathrm{2}\boldsymbol{{n}}+\mathrm{2}} \sqrt{\boldsymbol{{x}}} \\ $$$$\boldsymbol{{where}}\:\boldsymbol{{n}}=\mathrm{0}\:,\mathrm{1},\mathrm{2},\mathrm{3}….. \\ $$$$\boldsymbol{{and}}\:\boldsymbol{{it}}\:\boldsymbol{{gives}}\:\boldsymbol{{us}}\:+\sqrt{\boldsymbol{{x}}}\:\boldsymbol{{for}}\:\boldsymbol{{n}}={odd} \\ $$$$\boldsymbol{{and}}\:−\sqrt{\boldsymbol{{x}}\:}\:\boldsymbol{{for}}\:\boldsymbol{{n}}=\boldsymbol{{even}} \\ $$$$\boldsymbol{{this}}\:\boldsymbol{{is}}\:\boldsymbol{{our}}\:\boldsymbol{{convention}}\:\boldsymbol{{that}} \\ $$$$\sqrt{\mathrm{4}}\:\boldsymbol{{cosidered}}\:\boldsymbol{{as}}\:+\mathrm{2}\:\boldsymbol{{but}}\:\boldsymbol{{ingeneral}} \\ $$$$\boldsymbol{{that}}'\boldsymbol{{s}}\:\boldsymbol{{not}}\:\boldsymbol{{true}}\:\sqrt{\mathrm{4}}=\underset{−} {+}\mathrm{2}. \\ $$$$\boldsymbol{{it}}\:\boldsymbol{{just}}\:\boldsymbol{{depend}}\:\boldsymbol{{on}}\:\boldsymbol{{physical}} \\ $$$$\boldsymbol{{setuation}}\:\boldsymbol{{and}}\:\boldsymbol{{which}}\:\boldsymbol{{value}}\:\boldsymbol{{we}} \\ $$$$\boldsymbol{{wanted}}\:\boldsymbol{{to}}\:\boldsymbol{{take}}..\boldsymbol{{but}}\:\boldsymbol{{that}}\:\boldsymbol{{does}} \\ $$$$\boldsymbol{{not}}\:\boldsymbol{{mean}}\:\boldsymbol{{there}}\:\boldsymbol{{is}}\:\boldsymbol{{no}}\:\boldsymbol{{negetive}} \\ $$$$\boldsymbol{{value}}. \\ $$$$\boldsymbol{{remember}}\:\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)=\boldsymbol{{y}}\:\boldsymbol{{for}}\:\boldsymbol{{solving}} \\ $$$$\boldsymbol{{this}}\:\boldsymbol{{we}}\:\boldsymbol{{squaring}}\:\boldsymbol{{both}}\:\boldsymbol{{sides}}. \\ $$
