Question Number 127009 by BHOOPENDRA last updated on 26/Dec/20
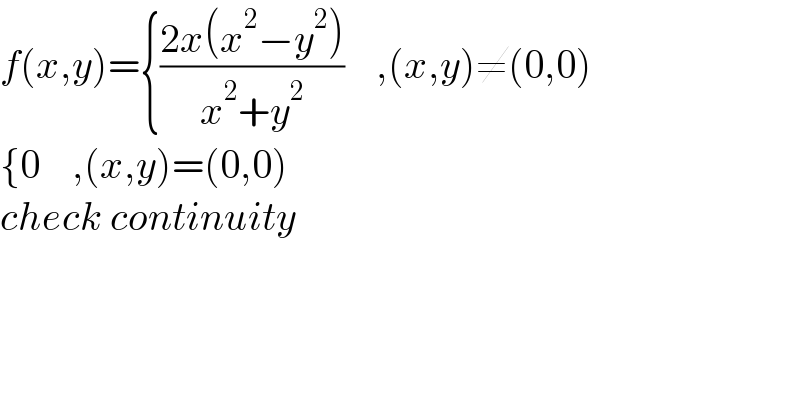
$${f}\left({x},{y}\right)=\left\{\frac{\mathrm{2}{x}\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:\:\:\:,\left({x},{y}\right)\neq\left(\mathrm{0},\mathrm{0}\right)\right. \\ $$$$\left\{\mathrm{0}\:\:\:\:,\left({x},{y}\right)=\left(\mathrm{0},\mathrm{0}\right)\right. \\ $$$${check}\:{continuity} \\ $$
Answered by Olaf last updated on 26/Dec/20
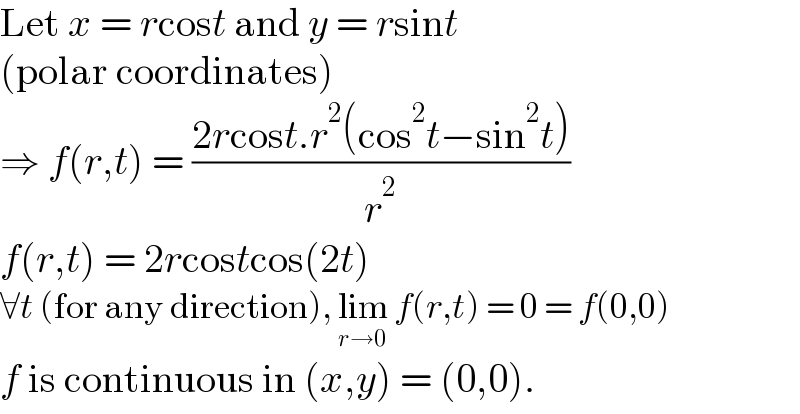
$$\mathrm{Let}\:{x}\:=\:{r}\mathrm{cos}{t}\:\mathrm{and}\:{y}\:=\:{r}\mathrm{sin}{t} \\ $$$$\left(\mathrm{polar}\:\mathrm{coordinates}\right) \\ $$$$\Rightarrow\:{f}\left({r},{t}\right)\:=\:\frac{\mathrm{2}{r}\mathrm{cos}{t}.{r}^{\mathrm{2}} \left(\mathrm{cos}^{\mathrm{2}} {t}−\mathrm{sin}^{\mathrm{2}} {t}\right)}{{r}^{\mathrm{2}} } \\ $$$${f}\left({r},{t}\right)\:=\:\mathrm{2}{r}\mathrm{cos}{t}\mathrm{cos}\left(\mathrm{2}{t}\right) \\ $$$$\forall{t}\:\left(\mathrm{for}\:\mathrm{any}\:\mathrm{direction}\right),\:\underset{{r}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{f}\left({r},{t}\right)\:=\:\mathrm{0}\:=\:{f}\left(\mathrm{0},\mathrm{0}\right) \\ $$$${f}\:\mathrm{is}\:\mathrm{continuous}\:\mathrm{in}\:\left({x},{y}\right)\:=\:\left(\mathrm{0},\mathrm{0}\right). \\ $$
Commented by BHOOPENDRA last updated on 26/Dec/20

$${thanks}\:{sir} \\ $$
