Menu Close

f-X-Y-f-E-F-f-E-f-F-f-is-1-to-1-I-think-it-is-not-true-since-let-x1-x2-x3-E-x3-x4-F-and-f-x1-f-x2-it-will-be-not-true-but-my-friend-say-by-q-p-f-is-not-1-to-1-f-E-F-f-E-f-F-and-tak

Tinku Tara 0 Comments
Pin




Question Number 156128 by aaaspots last updated on 08/Oct/21
f:X→Y f(E\F)=f(E)\f(F)⇒f is 1 to 1 I think it is not true since let x1 x2 x3∈E ,x3 x4∈F, and f(x1)=f( x2) it will be not true. but my friend say by ∼q⇒∼p f is not 1 to 1 ⇒f(E\F)≠f(E)\f(F),and take x1 x2∈X, f(x1)=f(x2)=y0 E={x1 ,x2} F={x2} and can proof it is true but I do not know which is true how to proof it?
$$\:{f}:{X}\rightarrow{Y} \\ $$$${f}\left({E}\backslash{F}\right)={f}\left({E}\right)\backslash{f}\left({F}\right)\Rightarrow{f}\:{is}\:\mathrm{1}\:{to}\:\mathrm{1} \\ $$$$ \\ $$$${I}\:{think}\:{it}\:{is}\:{not}\:{true}\: \\ $$$${since}\:{let}\:{x}\mathrm{1}\:{x}\mathrm{2}\:{x}\mathrm{3}\in{E}\:,{x}\mathrm{3}\:{x}\mathrm{4}\in{F}, \\ $$$${and}\:{f}\left({x}\mathrm{1}\right)={f}\left(\:{x}\mathrm{2}\right)\:{it}\:{will}\:{be}\:{not}\:{true}. \\ $$$$ \\ $$$${but}\:{my}\:{friend}\:{say}\:{by}\:\sim{q}\Rightarrow\sim{p} \\ $$$$\:{f}\:{is}\:{not}\:\mathrm{1}\:{to}\:\mathrm{1} \\ $$$$\Rightarrow{f}\left({E}\backslash{F}\right)\neq{f}\left({E}\right)\backslash{f}\left({F}\right),{and}\:{take} \\ $$$${x}\mathrm{1}\:{x}\mathrm{2}\in{X},\:{f}\left({x}\mathrm{1}\right)={f}\left({x}\mathrm{2}\right)={y}\mathrm{0} \\ $$$${E}=\left\{{x}\mathrm{1}\:,{x}\mathrm{2}\right\}\:{F}=\left\{{x}\mathrm{2}\right\} \\ $$$${and}\:\:{can}\:{proof}\:{it}\:{is}\:{true} \\ $$$${but}\:{I}\:{do}\:{not}\:{know}\:{which}\:{is}\:{true} \\ $$$${how}\:{to}\:{proof}\:{it}? \\ $$
Answered by TheSupreme last updated on 08/Oct/21
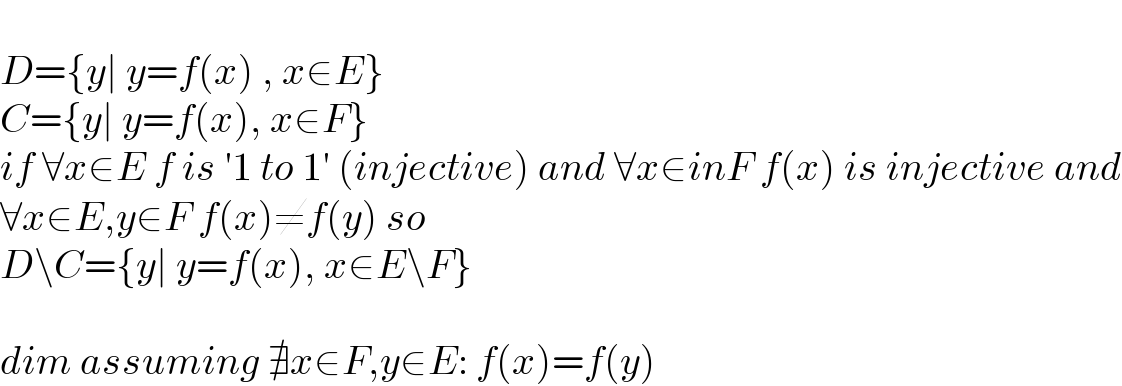
D={y∣ y=f(x) , x∈E} C={y∣ y=f(x), x∈F} if ∀x∈E f is ′1 to 1′ (injective) and ∀x∈inF f(x) is injective and ∀x∈E,y∈F f(x)≠f(y) so D\C={y∣ y=f(x), x∈E\F} dim assuming ∄x∈F,y∈E: f(x)=f(y)
$$ \\ $$$${D}=\left\{{y}\mid\:{y}={f}\left({x}\right)\:,\:{x}\in{E}\right\} \\ $$$${C}=\left\{{y}\mid\:{y}={f}\left({x}\right),\:{x}\in{F}\right\} \\ $$$${if}\:\forall{x}\in{E}\:{f}\:{is}\:'\mathrm{1}\:{to}\:\mathrm{1}'\:\left({injective}\right)\:{and}\:\forall{x}\in{inF}\:{f}\left({x}\right)\:{is}\:{injective}\:{and} \\ $$$$\forall{x}\in{E},{y}\in{F}\:{f}\left({x}\right)\neq{f}\left({y}\right)\:{so} \\ $$$${D}\backslash{C}=\left\{{y}\mid\:{y}={f}\left({x}\right),\:{x}\in{E}\backslash{F}\right\} \\ $$$$ \\ $$$${dim}\:{assuming}\:\nexists{x}\in{F},{y}\in{E}:\:{f}\left({x}\right)={f}\left({y}\right)\: \\ $$
Commented by aaaspots last updated on 08/Oct/21
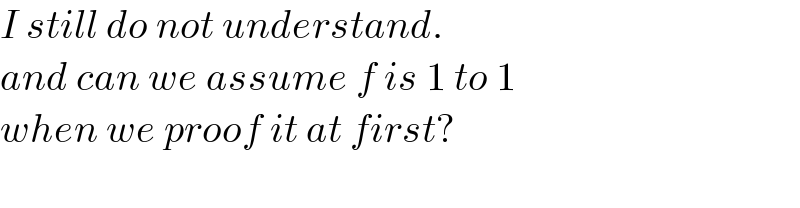
I still do not understand. and can we assume f is 1 to 1 when we proof it at first?
$${I}\:{still}\:{do}\:{not}\:{understand}. \\ $$$${and}\:{can}\:{we}\:{assume}\:{f}\:{is}\:\mathrm{1}\:{to}\:\mathrm{1}\: \\ $$$${when}\:{we}\:{proof}\:{it}\:{at}\:{first}? \\ $$$$ \\ $$
Commented by aaaspots last updated on 08/Oct/21
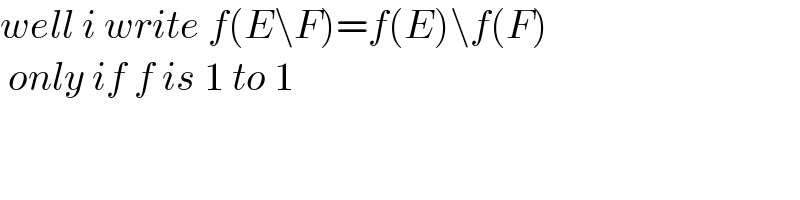
well i write f(E\F)=f(E)\f(F) only if f is 1 to 1
$${well}\:{i}\:{write}\:{f}\left({E}\backslash{F}\right)={f}\left({E}\right)\backslash{f}\left({F}\right)\: \\ $$$$\:{only}\:{if}\:{f}\:{is}\:\mathrm{1}\:{to}\:\mathrm{1} \\ $$
Commented by TheSupreme last updated on 08/Oct/21
f(x) is 1 to 1 only if the proposition (1) is true for all E,F ∈ D[f(x)] D is dominium, prop 1 is your question
$${f}\left({x}\right)\:{is}\:\mathrm{1}\:{to}\:\mathrm{1}\:{only}\:{if}\:{the}\:{proposition}\:\left(\mathrm{1}\right)\:{is}\:{true}\:{for}\:{all}\:{E},{F}\:\in\:{D}\left[{f}\left({x}\right)\right] \\ $$$${D}\:{is}\:{dominium},\:{prop}\:\mathrm{1}\:{is}\:{your}\:{question} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *