f-x-y-f-x-y-f-x-f-y-find-f-x-

Question Number 180407 by CrispyXYZ last updated on 12/Nov/22

$${f}\left({x}−{y}\right)+{f}\left({x}+{y}\right)={f}\left({x}\right){f}\left({y}\right) \\ $$$$\mathrm{find}\:{f}\left({x}\right) \\ $$

Answered by mahdipoor last updated on 12/Nov/22

x=0 y=0 ⇒ f(0)+f(0)=f(0)f(0) ⇒f(0)=0 or 2 x=x y=0 ⇒ f(x)+f(x)=f(0)f(x) ⇒ { ((if f(0)=0 ⇒ f(x)=0 ∀x)),((if f(0)=2 ⇒ f(x)=0 ∀x ⇒^(but) f(0)=2 and 0 ⇒ rejected)) :}

$${x}=\mathrm{0}\:\:\:{y}=\mathrm{0}\:\Rightarrow \\ $$$${f}\left(\mathrm{0}\right)+{f}\left(\mathrm{0}\right)={f}\left(\mathrm{0}\right){f}\left(\mathrm{0}\right)\:\Rightarrow{f}\left(\mathrm{0}\right)=\mathrm{0}\:\:{or}\:\:\mathrm{2} \\ $$$${x}={x}\:\:\:{y}=\mathrm{0}\:\Rightarrow \\ $$$${f}\left({x}\right)+{f}\left({x}\right)={f}\left(\mathrm{0}\right){f}\left({x}\right)\:\Rightarrow\: \\ $$$$\begin{cases}{{if}\:{f}\left(\mathrm{0}\right)=\mathrm{0}\:\Rightarrow\:{f}\left({x}\right)=\mathrm{0}\:\:\:\forall{x}}\\{{if}\:{f}\left(\mathrm{0}\right)=\mathrm{2}\:\Rightarrow\:{f}\left({x}\right)=\mathrm{0}\:\:\:\forall{x}\:\overset{{but}} {\Rightarrow}\:{f}\left(\mathrm{0}\right)=\mathrm{2}\:{and}\:\mathrm{0}\:\Rightarrow\:{rejected}}\end{cases} \\ $$

Answered by Rasheed.Sindhi last updated on 12/Nov/22

f(x−y)+f(x+y)=f(x)f(y)...(i) f(x)=? •y=0 in (i): 2f(x)=f(x)f(0)∙∙∙∙∙∙∙∙(ii) 2f(x)−f(x)f(0)=0 f(x)( 2−f(0) )=0 f(x)=0 ∨ f(0)=2 •f(0)=2 in (ii): 2f(x)=2f(x)→no useful result Hence determinant (((f(x)=0)))

$${f}\left({x}−{y}\right)+{f}\left({x}+{y}\right)={f}\left({x}\right){f}\left({y}\right)…\left({i}\right) \\ $$$${f}\left({x}\right)=? \\ $$$$\bullet{y}=\mathrm{0}\:{in}\:\left({i}\right): \\ $$$$\:\:\:\mathrm{2}{f}\left({x}\right)={f}\left({x}\right){f}\left(\mathrm{0}\right)\centerdot\centerdot\centerdot\centerdot\centerdot\centerdot\centerdot\centerdot\left({ii}\right) \\ $$$$\:\:\:\:\mathrm{2}{f}\left({x}\right)−{f}\left({x}\right){f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\:\:\:\:{f}\left({x}\right)\left(\:\mathrm{2}−{f}\left(\mathrm{0}\right)\:\right)=\mathrm{0} \\ $$$$\:\:\:\:{f}\left({x}\right)=\mathrm{0}\:\vee\:{f}\left(\mathrm{0}\right)=\mathrm{2} \\ $$$$\bullet{f}\left(\mathrm{0}\right)=\mathrm{2}\:{in}\:\left({ii}\right): \\ $$$$\:\:\:\:\mathrm{2}{f}\left({x}\right)=\mathrm{2}{f}\left({x}\right)\rightarrow{no}\:{useful}\:{result} \\ $$$$\mathcal{H}{ence} \\ $$$$\:\:\:\:\:\:\:\:\begin{array}{|c|}{{f}\left({x}\right)=\mathrm{0}}\\\hline\end{array} \\ $$

Commented by CrispyXYZ last updated on 13/Nov/22

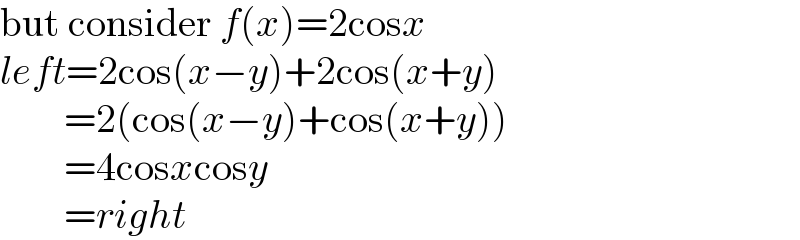
but consider f(x)=2cosx left=2cos(x−y)+2cos(x+y) =2(cos(x−y)+cos(x+y)) =4cosxcosy =right

$$\mathrm{but}\:\mathrm{consider}\:{f}\left({x}\right)=\mathrm{2cos}{x} \\ $$$${left}=\mathrm{2cos}\left({x}−{y}\right)+\mathrm{2cos}\left({x}+{y}\right) \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{2}\left(\mathrm{cos}\left({x}−{y}\right)+\mathrm{cos}\left({x}+{y}\right)\right) \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{4cos}{x}\mathrm{cos}{y} \\ $$$$\:\:\:\:\:\:\:\:={right} \\ $$

Commented by CrispyXYZ last updated on 13/Nov/22

Actually, f(x)=0∨f(x)=2∨f(x)=2cosx satisfy the condition

$$\mathrm{Actually},\:{f}\left({x}\right)=\mathrm{0}\vee{f}\left({x}\right)=\mathrm{2}\vee{f}\left({x}\right)=\mathrm{2cos}{x}\:\mathrm{satisfy}\:\mathrm{the}\:\mathrm{condition} \\ $$

Commented by Rasheed.Sindhi last updated on 13/Nov/22

ThanX! But now the question is what′s the process to reach f(x)=2cos(x) that is why I ′ve posted a more direct question: f(x−y)+f(x+y)=2f(x)f(y); f(x)=? the answer is f(x)=cos(x)

$$\mathcal{T}{han}\mathcal{X}!\:\mathcal{B}{ut}\:{now}\:{the}\:{question}\:{is} \\ $$$${what}'{s}\:{the}\:{process}\:{to}\:{reach}\:{f}\left({x}\right)=\mathrm{2cos}\left({x}\right) \\ $$$${that}\:{is}\:{why}\:{I}\:'{ve}\:{posted}\:{a}\:{more}\:{direct} \\ $$$${question}: \\ $$$${f}\left({x}−{y}\right)+{f}\left({x}+{y}\right)=\mathrm{2}{f}\left({x}\right){f}\left({y}\right);\:{f}\left({x}\right)=? \\ $$$${the}\:{answer}\:{is}\:{f}\left({x}\right)=\mathrm{cos}\left({x}\right)\: \\ $$

Facebook Tweet Pin

f-x-y-f-x-y-f-x-f-y-find-f-x-

Leave a Reply Cancel reply