Question Number 182649 by amin96 last updated on 12/Dec/22
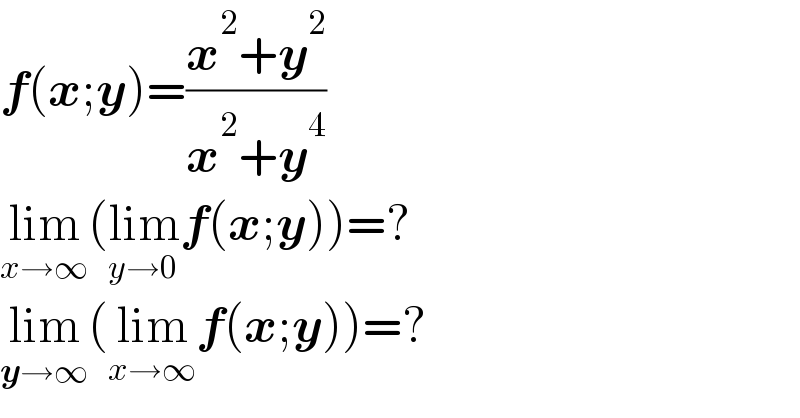
$$\boldsymbol{{f}}\left(\boldsymbol{{x}};\boldsymbol{{y}}\right)=\frac{\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{2}} }{\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{4}} }\:\:\:\:\: \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\boldsymbol{{f}}\left(\boldsymbol{{x}};\boldsymbol{{y}}\right)\right)=? \\ $$$$\underset{\boldsymbol{{y}}\rightarrow\infty} {\mathrm{lim}}\left(\underset{{x}\rightarrow\infty} {\mathrm{lim}}\boldsymbol{{f}}\left(\boldsymbol{{x}};\boldsymbol{{y}}\right)\right)=? \\ $$
Answered by FelipeLz last updated on 12/Dec/22
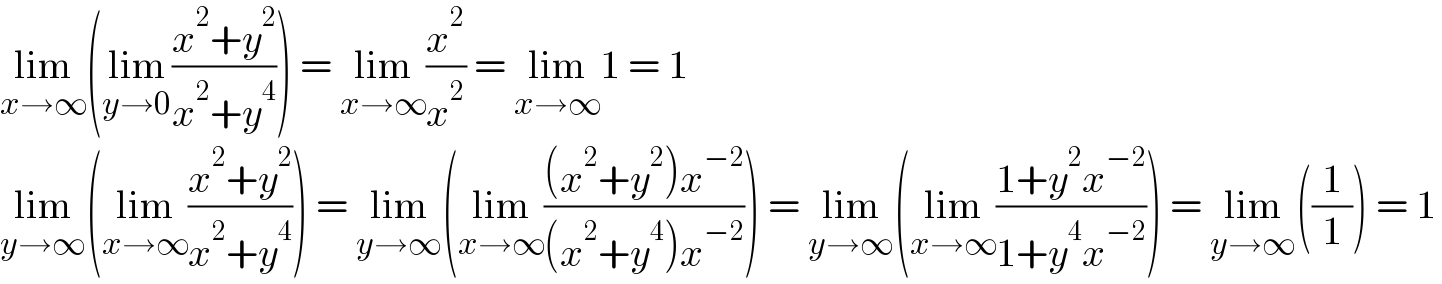
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{y}^{\mathrm{4}} }\right)\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}1}\:=\:\mathrm{1} \\ $$$$\underset{{y}\rightarrow\infty} {\mathrm{lim}}\left(\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{y}^{\mathrm{4}} }\right)\:=\:\underset{{y}\rightarrow\infty} {\mathrm{lim}}\left(\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right){x}^{−\mathrm{2}} }{\left({x}^{\mathrm{2}} +{y}^{\mathrm{4}} \right){x}^{−\mathrm{2}} }\right)\:=\:\underset{{y}\rightarrow\infty} {\mathrm{lim}}\left(\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}+{y}^{\mathrm{2}} {x}^{−\mathrm{2}} }{\mathrm{1}+{y}^{\mathrm{4}} {x}^{−\mathrm{2}} }\right)\:=\:\underset{{y}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\mathrm{1}}\right)\:=\:\mathrm{1} \\ $$
