Question Number 48161 by gunawan last updated on 20/Nov/18

$${f}\left({z}\right)=\frac{\mathrm{1}−{z}}{\mathrm{1}+{z}} \\ $$$${u}\left({x},{y}\right)=.. \\ $$$${v}\left({x},{y}\right)=.. \\ $$$$ \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 20/Nov/18
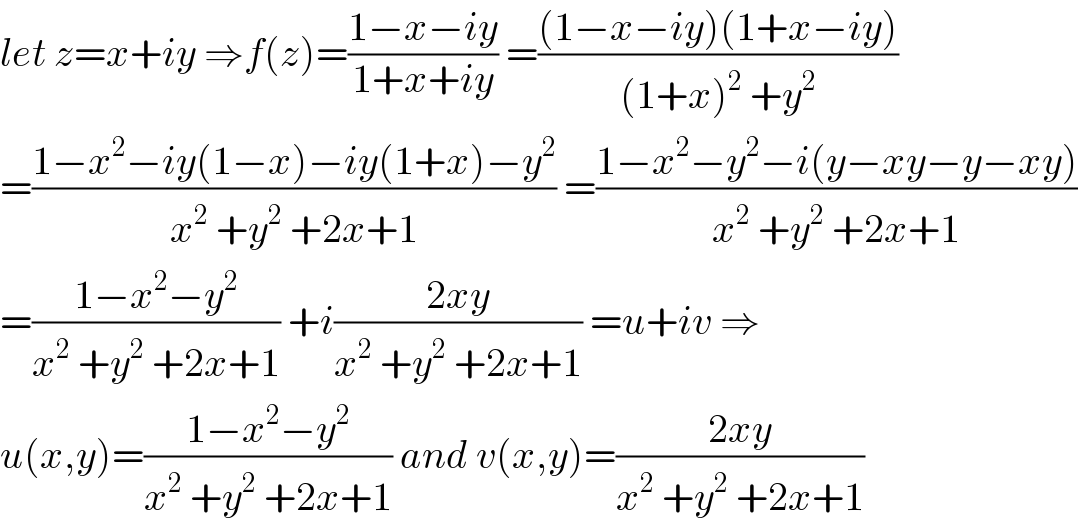
$${let}\:{z}={x}+{iy}\:\Rightarrow{f}\left({z}\right)=\frac{\mathrm{1}−{x}−{iy}}{\mathrm{1}+{x}+{iy}}\:=\frac{\left(\mathrm{1}−{x}−{iy}\right)\left(\mathrm{1}+{x}−{iy}\right)}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} \:+{y}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}−{x}^{\mathrm{2}} −{iy}\left(\mathrm{1}−{x}\right)−{iy}\left(\mathrm{1}+{x}\right)−{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \:+\mathrm{2}{x}+\mathrm{1}}\:=\frac{\mathrm{1}−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} −{i}\left({y}−{xy}−{y}−{xy}\right)}{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \:+\mathrm{2}{x}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \:+\mathrm{2}{x}+\mathrm{1}}\:+{i}\frac{\mathrm{2}{xy}}{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \:+\mathrm{2}{x}+\mathrm{1}}\:={u}+{iv}\:\Rightarrow \\ $$$${u}\left({x},{y}\right)=\frac{\mathrm{1}−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \:+\mathrm{2}{x}+\mathrm{1}}\:{and}\:{v}\left({x},{y}\right)=\frac{\mathrm{2}{xy}}{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \:+\mathrm{2}{x}+\mathrm{1}} \\ $$
Answered by ajfour last updated on 21/Nov/18
![f(z) = u+iv =(((1−x)−iy)/((1+x)+iy)) = (([(1−x)−iy][(1+x)−iy])/((1+x)^2 +y^2 )) = ((1−x^2 −y^2 )/((1+x)^2 +y^2 ))−i((2y)/((1+x^2 )+y^2 )) .](https://www.tinkutara.com/question/Q48163.png)
$${f}\left({z}\right)\:=\:{u}+{iv} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\left(\mathrm{1}−{x}\right)−{iy}}{\left(\mathrm{1}+{x}\right)+{iy}} \\ $$$$\:\:\:\:\:\:\:\:\:=\:\frac{\left[\left(\mathrm{1}−{x}\right)−{iy}\right]\left[\left(\mathrm{1}+{x}\right)−{iy}\right]}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} }−{i}\frac{\mathrm{2}{y}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)+{y}^{\mathrm{2}} }\:. \\ $$
Commented by gunawan last updated on 21/Nov/18

$$\mathrm{nice}\:\mathrm{Sir} \\ $$
