Question Number 51028 by gunawan last updated on 23/Dec/18

$${f}\left({z}\right)=\sqrt{{r}}\:{e}^{{i}\frac{\theta}{\mathrm{2}}} \\ $$$${f}'\left({z}\right)=…? \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 23/Dec/18

$${df}=\left(\frac{\partial{f}}{\partial{r}}\right)_{\theta} {dr}+\left(\frac{\partial{f}}{\partial\theta}\right)_{{r}} {d}\theta \\ $$$$={e}^{{i}\frac{\theta}{\mathrm{2}}} ×\frac{\mathrm{1}}{\mathrm{2}\sqrt{{r}}}{dr}+\sqrt{{r}}\:{e}^{\frac{{i}\theta}{\mathrm{2}}} ×\frac{{i}}{\mathrm{2}}{d}\theta \\ $$
Answered by MJS last updated on 23/Dec/18
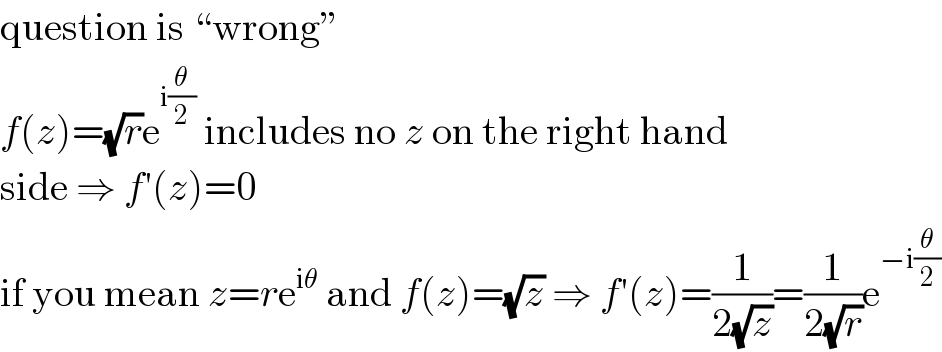
$$\mathrm{question}\:\mathrm{is}\:“\mathrm{wrong}'' \\ $$$${f}\left({z}\right)=\sqrt{{r}}\mathrm{e}^{\mathrm{i}\frac{\theta}{\mathrm{2}}} \:\mathrm{includes}\:\mathrm{no}\:{z}\:\mathrm{on}\:\mathrm{the}\:\mathrm{right}\:\mathrm{hand} \\ $$$$\mathrm{side}\:\Rightarrow\:{f}'\left({z}\right)=\mathrm{0} \\ $$$$\mathrm{if}\:\mathrm{you}\:\mathrm{mean}\:{z}={r}\mathrm{e}^{\mathrm{i}\theta} \:\mathrm{and}\:{f}\left({z}\right)=\sqrt{{z}}\:\Rightarrow\:{f}'\left({z}\right)=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{z}}}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{r}}}\mathrm{e}^{−\mathrm{i}\frac{\theta}{\mathrm{2}}} \\ $$
