Question Number 148599 by mathdanisur last updated on 29/Jul/21
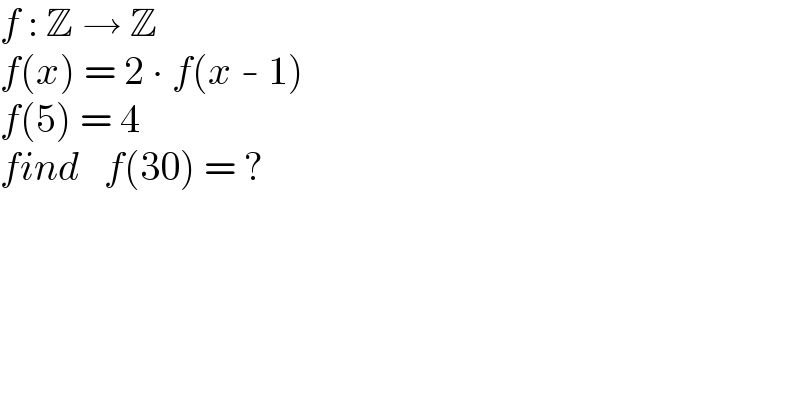
$${f}\::\:\mathbb{Z}\:\rightarrow\:\mathbb{Z} \\ $$$${f}\left({x}\right)\:=\:\mathrm{2}\:\centerdot\:{f}\left({x}\:-\:\mathrm{1}\right) \\ $$$${f}\left(\mathrm{5}\right)\:=\:\mathrm{4} \\ $$$${find}\:\:\:{f}\left(\mathrm{30}\right)\:=\:? \\ $$
Answered by Olaf_Thorendsen last updated on 29/Jul/21
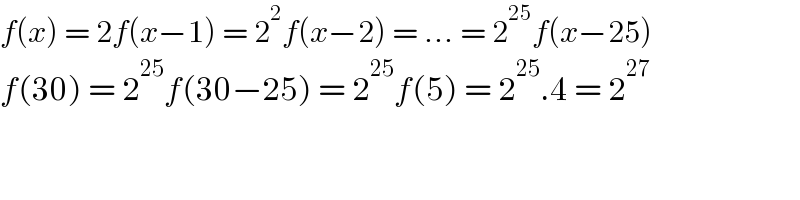
$${f}\left({x}\right)\:=\:\mathrm{2}{f}\left({x}−\mathrm{1}\right)\:=\:\mathrm{2}^{\mathrm{2}} {f}\left({x}−\mathrm{2}\right)\:=\:…\:=\:\mathrm{2}^{\mathrm{25}} {f}\left({x}−\mathrm{25}\right) \\ $$$${f}\left(\mathrm{30}\right)\:=\:\mathrm{2}^{\mathrm{25}} {f}\left(\mathrm{30}−\mathrm{25}\right)\:=\:\mathrm{2}^{\mathrm{25}} {f}\left(\mathrm{5}\right)\:=\:\mathrm{2}^{\mathrm{25}} .\mathrm{4}\:=\:\mathrm{2}^{\mathrm{27}} \\ $$
Commented by mathdanisur last updated on 29/Jul/21

$${Thank}\:{you}\:{Ser} \\ $$
Answered by Ar Brandon last updated on 29/Jul/21
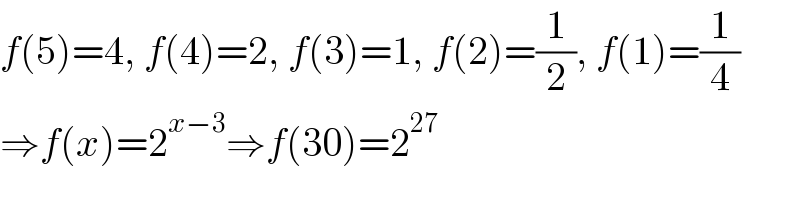
$${f}\left(\mathrm{5}\right)=\mathrm{4},\:{f}\left(\mathrm{4}\right)=\mathrm{2},\:{f}\left(\mathrm{3}\right)=\mathrm{1},\:{f}\left(\mathrm{2}\right)=\frac{\mathrm{1}}{\mathrm{2}},\:{f}\left(\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow{f}\left({x}\right)=\mathrm{2}^{{x}−\mathrm{3}} \Rightarrow{f}\left(\mathrm{30}\right)=\mathrm{2}^{\mathrm{27}} \\ $$
Commented by mathdanisur last updated on 29/Jul/21

$${Thank}\:{you}\:{Ser} \\ $$
Answered by mathmax by abdo last updated on 29/Jul/21
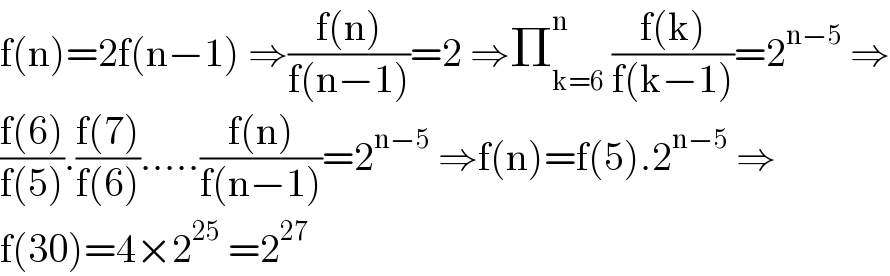
$$\mathrm{f}\left(\mathrm{n}\right)=\mathrm{2f}\left(\mathrm{n}−\mathrm{1}\right)\:\Rightarrow\frac{\mathrm{f}\left(\mathrm{n}\right)}{\mathrm{f}\left(\mathrm{n}−\mathrm{1}\right)}=\mathrm{2}\:\Rightarrow\prod_{\mathrm{k}=\mathrm{6}} ^{\mathrm{n}} \:\frac{\mathrm{f}\left(\mathrm{k}\right)}{\mathrm{f}\left(\mathrm{k}−\mathrm{1}\right)}=\mathrm{2}^{\mathrm{n}−\mathrm{5}} \:\Rightarrow \\ $$$$\frac{\mathrm{f}\left(\mathrm{6}\right)}{\mathrm{f}\left(\mathrm{5}\right)}.\frac{\mathrm{f}\left(\mathrm{7}\right)}{\mathrm{f}\left(\mathrm{6}\right)}…..\frac{\mathrm{f}\left(\mathrm{n}\right)}{\mathrm{f}\left(\mathrm{n}−\mathrm{1}\right)}=\mathrm{2}^{\mathrm{n}−\mathrm{5}} \:\Rightarrow\mathrm{f}\left(\mathrm{n}\right)=\mathrm{f}\left(\mathrm{5}\right).\mathrm{2}^{\mathrm{n}−\mathrm{5}} \:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{30}\right)=\mathrm{4}×\mathrm{2}^{\mathrm{25}} \:=\mathrm{2}^{\mathrm{27}} \\ $$
Commented by mathdanisur last updated on 29/Jul/21

$${Thank}\:{you}\:{Ser} \\ $$
