Menu Close

factor-x-3-x-2-x-1-3-and-x-3-x-2-x-1-3-and-x-3-x-2-x-1-3-

Tinku Tara 0 Comments
Pin




Question Number 50925 by kaivan.ahmadi last updated on 22/Dec/18
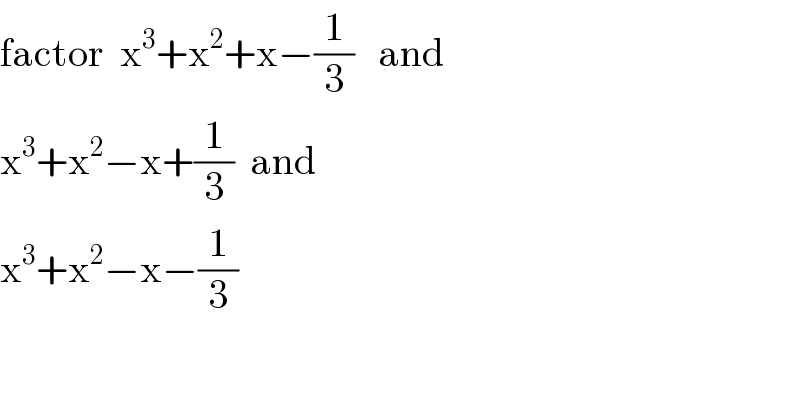
factor x^3 +x^2 +x−(1/3) and x^3 +x^2 −x+(1/3) and x^3 +x^2 −x−(1/3)
$$\mathrm{factor}\:\:\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\frac{\mathrm{1}}{\mathrm{3}}\:\:\:\mathrm{and} \\ $$$$\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\frac{\mathrm{1}}{\mathrm{3}}\:\:\mathrm{and} \\ $$$$\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Commented by Abdo msup. last updated on 23/Dec/18
let p(x)=x^3 +x^2 +x−(1/3) let find the roots changement x=t−(1/3) give p(x)=(t−(1/3))^3 +(t−(1/3))^2 +t−(2/3) =t^3 −3 t^2 .(1/3) +3t (1/9) −(1/(27)) + t^2 −(2/3)t +(1/9) +t−(2/3) =t^3 −t^2 +(t/3) +t^2 +(1/3)t +((−1+3−18)/(27)) =t^3 +(2/3)t −((16)/(27)) =g(t) let solve g(t)=0 with t=u+v we get (u+v)^3 +(2/3)(u+v)−((16)/(27)) =0 ⇒ u^3 +v^3 +3uv(u+v) +(2/3)(u+v)−((16)/(27)) =0 ⇒ u^3 +v^3 −((16)/(27)) =0 and 3uv +(2/3) =0 ⇒ u^3 +v^3 =((16)/(27)) and uv=−(2/9) ⇒ u^3 +v^3 =((16)/(27)) and u^3 v^3 =((−8)/(729)) so u^3 and v^3 are solution of the equation z^2 −((16)/(27)) z −(8/(729)) =0... Δ =(−((16)/(27)))^2 +((32)/(729)) >0 ⇒z_1 =((((16)/(27))+(√(((16^2 )/(27^2 ))+((32)/(729)))))/2) z_2 =... be continued...
$${let}\:{p}\left({x}\right)={x}^{\mathrm{3}} \:+{x}^{\mathrm{2}} \:+{x}−\frac{\mathrm{1}}{\mathrm{3}}\:{let}\:{find}\:{the}\:{roots}\:{changement}\:{x}={t}−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${give}\:{p}\left({x}\right)=\left({t}−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{3}} \:+\left({t}−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} \:+{t}−\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$={t}^{\mathrm{3}} \:−\mathrm{3}\:{t}^{\mathrm{2}} .\frac{\mathrm{1}}{\mathrm{3}}\:+\mathrm{3}{t}\:\frac{\mathrm{1}}{\mathrm{9}}\:−\frac{\mathrm{1}}{\mathrm{27}}\:+\:{t}^{\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{3}}{t}\:\:+\frac{\mathrm{1}}{\mathrm{9}}\:+{t}−\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$={t}^{\mathrm{3}} \:−{t}^{\mathrm{2}} \:+\frac{{t}}{\mathrm{3}}\:+{t}^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{3}}{t}\:\:+\frac{−\mathrm{1}+\mathrm{3}−\mathrm{18}}{\mathrm{27}} \\ $$$$={t}^{\mathrm{3}} \:+\frac{\mathrm{2}}{\mathrm{3}}{t}\:\:−\frac{\mathrm{16}}{\mathrm{27}}\:\:={g}\left({t}\right)\:{let}\:{solve}\:{g}\left({t}\right)=\mathrm{0}\:\:{with}\:{t}={u}+{v} \\ $$$${we}\:{get}\:\left({u}+{v}\right)^{\mathrm{3}} \:+\frac{\mathrm{2}}{\mathrm{3}}\left({u}+{v}\right)−\frac{\mathrm{16}}{\mathrm{27}}\:=\mathrm{0}\:\Rightarrow \\ $$$${u}^{\mathrm{3}} \:+{v}^{\mathrm{3}} \:+\mathrm{3}{uv}\left({u}+{v}\right)\:+\frac{\mathrm{2}}{\mathrm{3}}\left({u}+{v}\right)−\frac{\mathrm{16}}{\mathrm{27}}\:=\mathrm{0}\:\Rightarrow \\ $$$${u}^{\mathrm{3}} \:+{v}^{\mathrm{3}} −\frac{\mathrm{16}}{\mathrm{27}}\:=\mathrm{0}\:{and}\:\:\mathrm{3}{uv}\:+\frac{\mathrm{2}}{\mathrm{3}}\:=\mathrm{0}\:\Rightarrow \\ $$$${u}^{\mathrm{3}} \:+{v}^{\mathrm{3}} \:=\frac{\mathrm{16}}{\mathrm{27}}\:{and}\:{uv}=−\frac{\mathrm{2}}{\mathrm{9}}\:\Rightarrow \\ $$$${u}^{\mathrm{3}} \:+{v}^{\mathrm{3}} =\frac{\mathrm{16}}{\mathrm{27}}\:{and}\:\:{u}^{\mathrm{3}} {v}^{\mathrm{3}} =\frac{−\mathrm{8}}{\mathrm{729}}\:\:{so}\:{u}^{\mathrm{3}} \:{and}\:{v}^{\mathrm{3}} \:{are}\:{solution} \\ $$$${of}\:{the}\:{equation}\:{z}^{\mathrm{2}} −\frac{\mathrm{16}}{\mathrm{27}}\:{z}\:−\frac{\mathrm{8}}{\mathrm{729}}\:=\mathrm{0}… \\ $$$$\Delta\:=\left(−\frac{\mathrm{16}}{\mathrm{27}}\right)^{\mathrm{2}} \:+\frac{\mathrm{32}}{\mathrm{729}}\:>\mathrm{0}\:\Rightarrow{z}_{\mathrm{1}} =\frac{\frac{\mathrm{16}}{\mathrm{27}}+\sqrt{\frac{\mathrm{16}^{\mathrm{2}} }{\mathrm{27}^{\mathrm{2}} }+\frac{\mathrm{32}}{\mathrm{729}}}}{\mathrm{2}} \\ $$$${z}_{\mathrm{2}} =…\:{be}\:{continued}… \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *