Question Number 29458 by prof Abdo imad last updated on 08/Feb/18
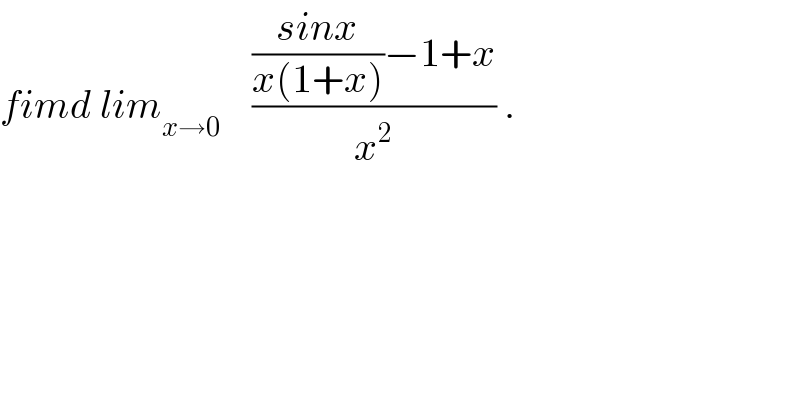
$${fimd}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\:\frac{\frac{{sinx}}{{x}\left(\mathrm{1}+{x}\right)}−\mathrm{1}+{x}}{{x}^{\mathrm{2}} }\:. \\ $$
Commented by prof Abdo imad last updated on 13/Feb/18
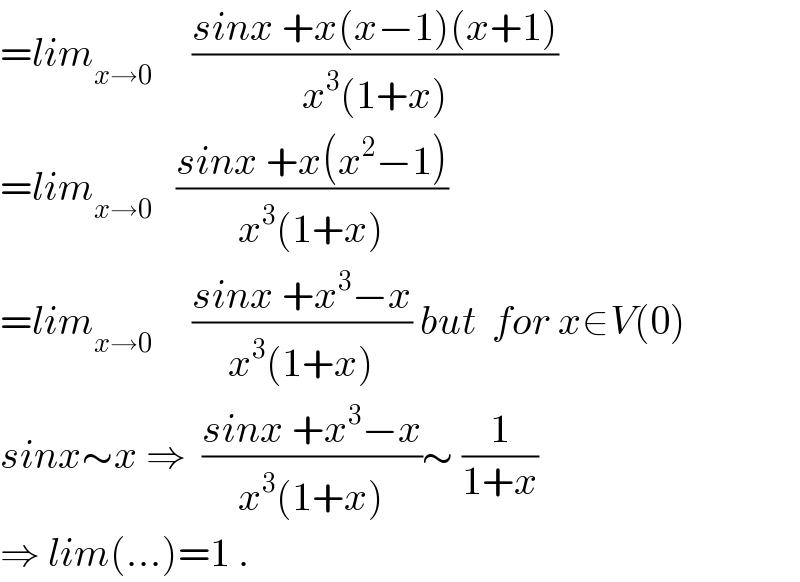
$$={lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\:\:\frac{{sinx}\:+{x}\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)}{{x}^{\mathrm{3}} \left(\mathrm{1}+{x}\right)} \\ $$$$={lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\frac{{sinx}\:+{x}\left({x}^{\mathrm{2}} −\mathrm{1}\right)}{{x}^{\mathrm{3}} \left(\mathrm{1}+{x}\right)} \\ $$$$={lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\:\:\frac{{sinx}\:+{x}^{\mathrm{3}} −{x}}{{x}^{\mathrm{3}} \left(\mathrm{1}+{x}\right)}\:{but}\:\:{for}\:{x}\in{V}\left(\mathrm{0}\right) \\ $$$${sinx}\sim{x}\:\Rightarrow\:\:\frac{{sinx}\:+{x}^{\mathrm{3}} −{x}}{{x}^{\mathrm{3}} \left(\mathrm{1}+{x}\right)}\sim\:\frac{\mathrm{1}}{\mathrm{1}+{x}} \\ $$$$\Rightarrow\:{lim}\left(…\right)=\mathrm{1}\:. \\ $$
