Menu Close

find-0-1-1-x-2-1-x-3-dx-

Tinku Tara 0 Comments
Pin




Question Number 42792 by maxmathsup by imad last updated on 02/Sep/18
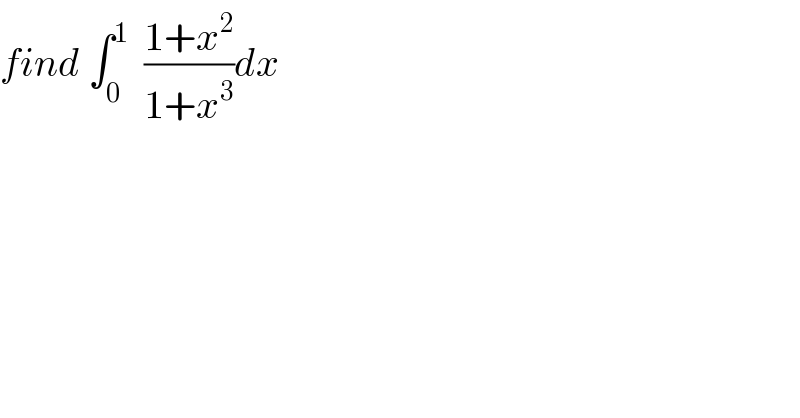
find ∫_0 ^1 ((1+x^2 )/(1+x^3 ))dx
find∫011+x21+x3dx
Commented by behi83417@gmail.com last updated on 03/Sep/18
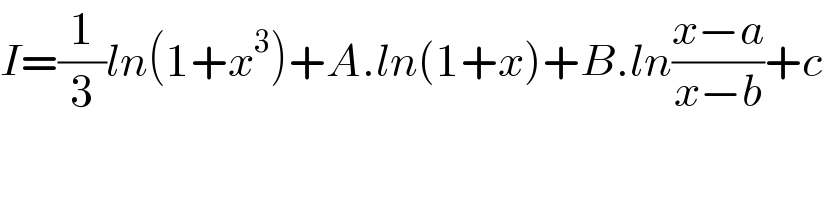
I=(1/3)ln(1+x^3 )+A.ln(1+x)+B.ln((x−a)/(x−b))+c
I=13ln(1+x3)+A.ln(1+x)+B.lnx−ax−b+c
Answered by tanmay.chaudhury50@gmail.com last updated on 04/Sep/18
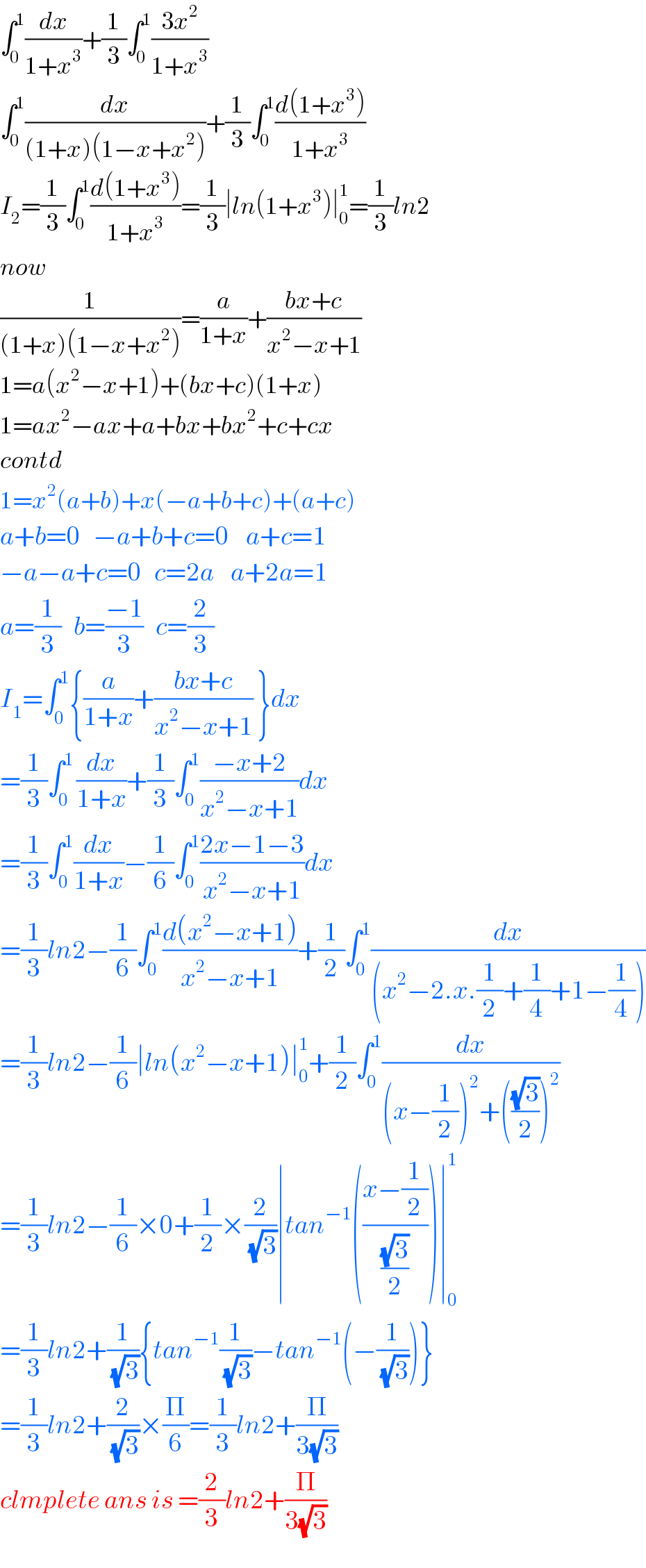
∫_0 ^1 (dx/(1+x^3 ))+(1/3)∫_0 ^1 ((3x^2 )/(1+x^3 )) ∫_0 ^1 (dx/((1+x)(1−x+x^2 )))+(1/3)∫_0 ^1 ((d(1+x^3 ))/(1+x^3 )) I_2 =(1/3)∫_0 ^1 ((d(1+x^3 ))/(1+x^3 ))=(1/3)∣ln(1+x^3 )∣_0 ^1 =(1/3)ln2 now (1/((1+x)(1−x+x^2 )))=(a/(1+x))+((bx+c)/(x^2 −x+1)) 1=a(x^2 −x+1)+(bx+c)(1+x) 1=ax^2 −ax+a+bx+bx^2 +c+cx contd 1=x^2 (a+b)+x(−a+b+c)+(a+c) a+b=0 −a+b+c=0 a+c=1 −a−a+c=0 c=2a a+2a=1 a=(1/3) b=((−1)/3) c=(2/3) I_1 =∫_0 ^1 {(a/(1+x))+((bx+c)/(x^2 −x+1)) }dx =(1/3)∫_(0 ) ^1 (dx/(1+x))+(1/3)∫_0 ^1 ((−x+2)/(x^2 −x+1))dx =(1/3)∫_0 ^1 (dx/(1+x))−(1/6)∫_0 ^1 ((2x−1−3)/(x^2 −x+1))dx =(1/3)ln2−(1/6)∫_0 ^1 ((d(x^2 −x+1))/(x^2 −x+1))+(1/2)∫_0 ^1 (dx/((x^2 −2.x.(1/2)+(1/4)+1−(1/4)))) =(1/3)ln2−(1/6)∣ln(x^2 −x+1)∣_0 ^1 +(1/2)∫_0 ^1 (dx/((x−(1/2))^2 +(((√3)/2))^2 )) =(1/3)ln2−(1/6)×0+(1/2)×(2/( (√3)))∣tan^(−1) (((x−(1/2))/((√3)/2)))∣_0 ^1 =(1/3)ln2+(1/( (√3))){tan^(−1) (1/( (√3)))−tan^(−1) (−(1/( (√3))))} =(1/3)ln2+(2/( (√3)))×(Π/6)=(1/3)ln2+(Π/(3(√3))) clmplete ans is =(2/3)ln2+(Π/(3(√3)))
∫01dx1+x3+13∫013x21+x3∫01dx(1+x)(1−x+x2)+13∫01d(1+x3)1+x3I2=13∫01d(1+x3)1+x3=13∣ln(1+x3)∣01=13ln2now1(1+x)(1−x+x2)=a1+x+bx+cx2−x+11=a(x2−x+1)+(bx+c)(1+x)1=ax2−ax+a+bx+bx2+c+cxcontd1=x2(a+b)+x(−a+b+c)+(a+c)a+b=0−a+b+c=0a+c=1−a−a+c=0c=2aa+2a=1a=13b=−13c=23I1=∫01{a1+x+bx+cx2−x+1}dx=13∫01dx1+x+13∫01−x+2x2−x+1dx=13∫01dx1+x−16∫012x−1−3x2−x+1dx=13ln2−16∫01d(x2−x+1)x2−x+1+12∫01dx(x2−2.x.12+14+1−14)=13ln2−16∣ln(x2−x+1)∣01+12∫01dx(x−12)2+(32)2=13ln2−16×0+12×23∣tan−1(x−1232)∣01=13ln2+13{tan−113−tan−1(−13)}=13ln2+23×Π6=13ln2+Π33clmpleteansis=23ln2+Π33

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *