Question Number 61039 by mathsolverby Abdo last updated on 28/May/19
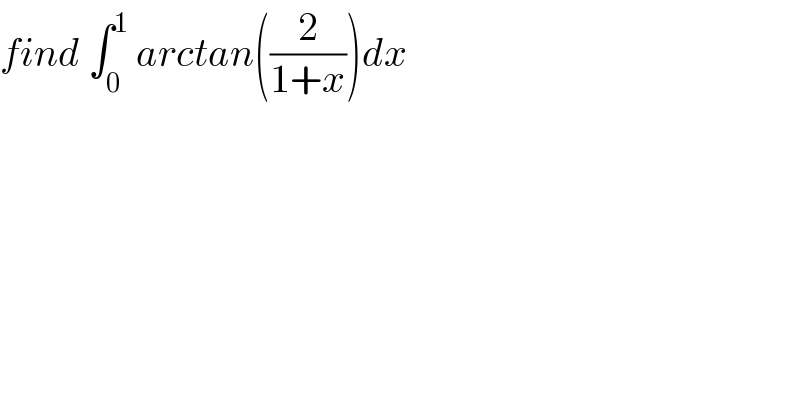
$${find}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{arctan}\left(\frac{\mathrm{2}}{\mathrm{1}+{x}}\right){dx} \\ $$
Commented by maxmathsup by imad last updated on 29/May/19
![let A =∫_0 ^1 arctn((2/(1+x)))dx by parts u^′ =1 and v=arctan((2/(1+x))) ⇒ v^′ =(((−2)/((1+x)^2 ))/(1+((2/(1+x)))^2 )) =((−2)/((1+x^2 ){1+(4/((1+x)^2 ))})) =((−2)/(1+x^2 +4)) =((−2)/(x^2 +5)) ⇒ A =[x arctan((2/(1+x)))]_0 ^1 −∫_0 ^1 ((−2x)/(x^2 +5)) dx =(π/4) +∫_0 ^1 ((2x)/(x^2 +5)) dx =(π/4) +[ln(x^2 +5)]_0 ^1 =(π/4) +ln(6)−ln(5) .](https://www.tinkutara.com/question/Q61145.png)
$${let}\:{A}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:{arctn}\left(\frac{\mathrm{2}}{\mathrm{1}+{x}}\right){dx}\:\:\:{by}\:{parts}\:\:{u}^{'} =\mathrm{1}\:\:{and}\:{v}={arctan}\left(\frac{\mathrm{2}}{\mathrm{1}+{x}}\right)\:\Rightarrow \\ $$$${v}^{'} \:=\frac{\frac{−\mathrm{2}}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }}{\mathrm{1}+\left(\frac{\mathrm{2}}{\mathrm{1}+{x}}\right)^{\mathrm{2}} }\:=\frac{−\mathrm{2}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left\{\mathrm{1}+\frac{\mathrm{4}}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }\right\}}\:=\frac{−\mathrm{2}}{\mathrm{1}+{x}^{\mathrm{2}} \:+\mathrm{4}}\:=\frac{−\mathrm{2}}{{x}^{\mathrm{2}} \:+\mathrm{5}}\:\Rightarrow \\ $$$${A}\:=\left[{x}\:{arctan}\left(\frac{\mathrm{2}}{\mathrm{1}+{x}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{−\mathrm{2}{x}}{{x}^{\mathrm{2}} \:+\mathrm{5}}\:{dx}\:=\frac{\pi}{\mathrm{4}}\:+\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} \:+\mathrm{5}}\:{dx} \\ $$$$=\frac{\pi}{\mathrm{4}}\:+\left[{ln}\left({x}^{\mathrm{2}} \:+\mathrm{5}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\frac{\pi}{\mathrm{4}}\:+{ln}\left(\mathrm{6}\right)−{ln}\left(\mathrm{5}\right)\:. \\ $$
