Question Number 96962 by mathmax by abdo last updated on 05/Jun/20
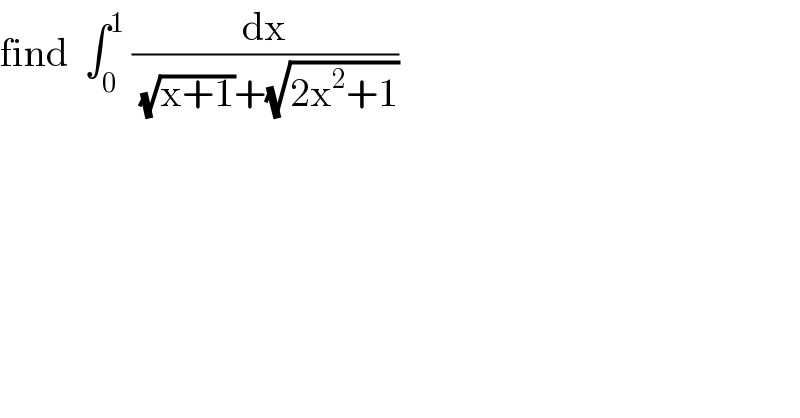
$$\mathrm{find}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{x}+\mathrm{1}}+\sqrt{\mathrm{2x}^{\mathrm{2}} +\mathrm{1}}} \\ $$
Answered by MJS last updated on 06/Jun/20
![∫(dx/( (√(x+1))+(√(2x^2 +1))))=∫((√(2x^2 +1))/(2x^2 −x))dx−∫((√(x+1))/(2x^2 −x))dx ∫((√(2x^2 +1))/(2x^2 −x))dx= [t=(√2)x+(√(2x^2 +1)) → dx=((√(2x^2 +1))/(2x+(√(2(2x^2 +1)))))] =∫((t^4 +2t^2 +1)/(t(t^2 −1)(t^2 −(√2)t−1)))dt= =((√6)/2)∫(dt/(t−(((√6)+(√2))/2)))−((√6)/2)∫(dt/(t+(((√6)−(√2))/2)))−∫(dt/(t−1))+∫(dt/(t+1))+((√2)/2)∫(dt/t)= =((√6)/2)ln (((√2)t−1−(√3))/( (√2)t−1+(√3))) +ln ((t+1)/(t−1)) +((√2)/2)ln t −∫((√(x+1))/(2x^2 −x))dx= [u=(√(x+1)) → dx=2(√(x+1))du] =−2∫(u^2 /((u^2 −1)(2u^2 −3)))du= =−((√6)/2)∫(du/(u−((√6)/2)))+((√6)/2)∫(du/(u+((√6)/2)))+∫(du/(u−1))−∫(du/(u+1))= =((√6)/2)ln (((√2)u+(√3))/( (√2)u−(√3))) +ln ((u−1)/(u+1)) the problem is now, the sum of these integrals seems to diverge but approximation of the original integral gives ≈.409087](https://www.tinkutara.com/question/Q97034.png)
$$\int\frac{{dx}}{\:\sqrt{{x}+\mathrm{1}}+\sqrt{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}}=\int\frac{\sqrt{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}}{\mathrm{2}{x}^{\mathrm{2}} −{x}}{dx}−\int\frac{\sqrt{{x}+\mathrm{1}}}{\mathrm{2}{x}^{\mathrm{2}} −{x}}{dx} \\ $$$$ \\ $$$$\int\frac{\sqrt{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}}{\mathrm{2}{x}^{\mathrm{2}} −{x}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{\mathrm{2}}{x}+\sqrt{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}\:\rightarrow\:{dx}=\frac{\sqrt{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}}{\mathrm{2}{x}+\sqrt{\mathrm{2}\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\right)}}\right] \\ $$$$=\int\frac{{t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{2}} +\mathrm{1}}{{t}\left({t}^{\mathrm{2}} −\mathrm{1}\right)\left({t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}−\mathrm{1}\right)}{dt}= \\ $$$$=\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}\int\frac{{dt}}{{t}−\frac{\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}}{\mathrm{2}}}−\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}\int\frac{{dt}}{{t}+\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\mathrm{2}}}−\int\frac{{dt}}{{t}−\mathrm{1}}+\int\frac{{dt}}{{t}+\mathrm{1}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\int\frac{{dt}}{{t}}= \\ $$$$=\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}\mathrm{ln}\:\frac{\sqrt{\mathrm{2}}{t}−\mathrm{1}−\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{2}}{t}−\mathrm{1}+\sqrt{\mathrm{3}}}\:+\mathrm{ln}\:\frac{{t}+\mathrm{1}}{{t}−\mathrm{1}}\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{ln}\:{t} \\ $$$$ \\ $$$$−\int\frac{\sqrt{{x}+\mathrm{1}}}{\mathrm{2}{x}^{\mathrm{2}} −{x}}{dx}= \\ $$$$\:\:\:\:\:\left[{u}=\sqrt{{x}+\mathrm{1}}\:\rightarrow\:{dx}=\mathrm{2}\sqrt{{x}+\mathrm{1}}{du}\right] \\ $$$$=−\mathrm{2}\int\frac{{u}^{\mathrm{2}} }{\left({u}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{2}{u}^{\mathrm{2}} −\mathrm{3}\right)}{du}= \\ $$$$=−\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}\int\frac{{du}}{{u}−\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}}+\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}\int\frac{{du}}{{u}+\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}}+\int\frac{{du}}{{u}−\mathrm{1}}−\int\frac{{du}}{{u}+\mathrm{1}}= \\ $$$$=\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}\mathrm{ln}\:\frac{\sqrt{\mathrm{2}}{u}+\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{2}}{u}−\sqrt{\mathrm{3}}}\:+\mathrm{ln}\:\frac{{u}−\mathrm{1}}{{u}+\mathrm{1}} \\ $$$$ \\ $$$$\mathrm{the}\:\mathrm{problem}\:\mathrm{is}\:\mathrm{now},\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{these}\:\mathrm{integrals} \\ $$$$\mathrm{seems}\:\mathrm{to}\:\mathrm{diverge}\:\mathrm{but}\:\mathrm{approximation}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{original}\:\mathrm{integral}\:\mathrm{gives}\:\approx.\mathrm{409087} \\ $$
Commented by mathmax by abdo last updated on 06/Jun/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$
