Question Number 30765 by abdo imad last updated on 25/Feb/18
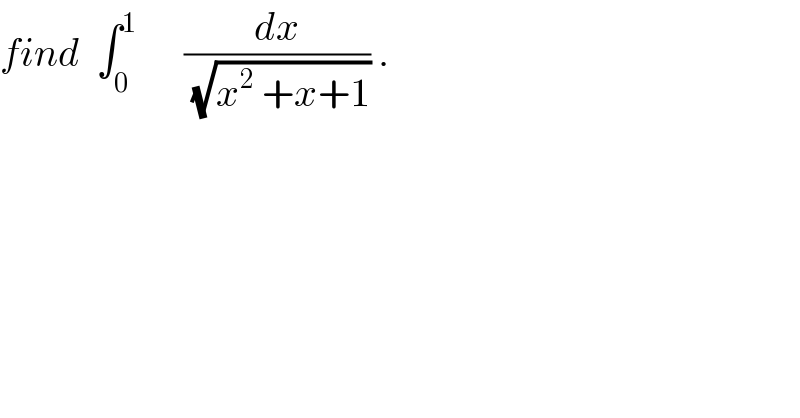
$${find}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\:\:\frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}}}\:. \\ $$
Commented by abdo imad last updated on 26/Feb/18
![we have x^2 +x +1=(x+(1/2))^2 +(3/4) let put I=∫_0 ^1 (dx/( (√(x^2 +x+1)))) the ch. x+(1/2)=((√3)/2)t ⇒I= ∫_(1/( (√3))) ^(√3) (1/( (√((3/4)t^2 +(3/4))))) ((√3)/2)dt I= ∫_(1/( (√3))) ^(√3) (dt/( (√(t^2 +1)))) =[ln(t +(√(t^2 +1)) )]_(1/( (√3))) ^(√3) =ln((√3) +2) −ln((1/( (√3))) +(√(4/3)) ) =ln(2+(√3) )−ln(((1+2)/( (√3))))=ln(2+(√3))−ln((√(3))) .](https://www.tinkutara.com/question/Q30844.png)
$${we}\:{have}\:{x}^{\mathrm{2}} \:+{x}\:+\mathrm{1}=\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}\:{let}\:{put}\:{I}=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}}} \\ $$$${the}\:{ch}.\:{x}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{t}\:\Rightarrow{I}=\:\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\sqrt{\mathrm{3}}} \:\:\:\frac{\mathrm{1}}{\:\sqrt{\frac{\mathrm{3}}{\mathrm{4}}{t}^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}}}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{dt} \\ $$$${I}=\:\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\sqrt{\mathrm{3}}} \:\:\:\:\:\:\:\frac{{dt}}{\:\sqrt{{t}^{\mathrm{2}} \:+\mathrm{1}}}\:=\left[{ln}\left({t}\:+\sqrt{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\right)\right]_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\sqrt{\mathrm{3}}} \\ $$$$={ln}\left(\sqrt{\mathrm{3}}\:\:+\mathrm{2}\right)\:−{ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:+\sqrt{\frac{\mathrm{4}}{\mathrm{3}}}\:\right) \\ $$$$={ln}\left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right)−{ln}\left(\frac{\mathrm{1}+\mathrm{2}}{\:\sqrt{\mathrm{3}}}\right)={ln}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)−{ln}\left(\sqrt{\left.\mathrm{3}\right)}\:.\right. \\ $$
