Question Number 27616 by abdo imad last updated on 10/Jan/18
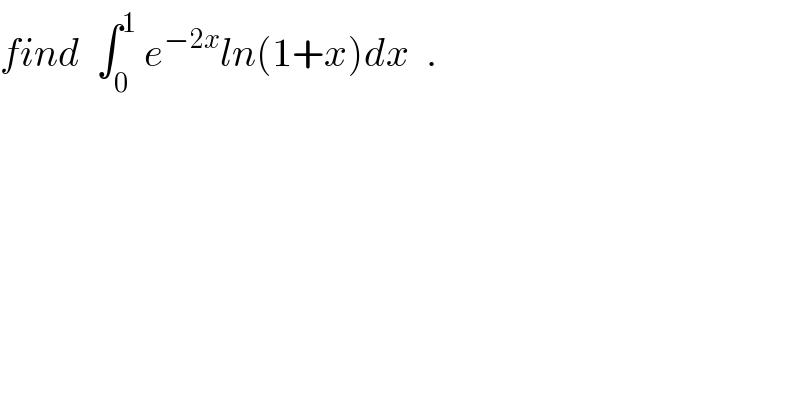
$${find}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{−\mathrm{2}{x}} {ln}\left(\mathrm{1}+{x}\right){dx}\:\:. \\ $$
Commented by abdo imad last updated on 15/Jan/18
![let put I= ∫_0 ^1 e^(−2x) ln(1+x)dx let integrate par parts I= [ ((−1)/2) e^(−2x) ln(1+x)]_0 ^1 − ∫_0 ^1 ((−1)/2) e^(−2x) (dx/(1+x)) =−(1/2) e^(−2) ln(2 ) + (1/2) ∫_0 ^1 (e^(−2x) /(1+x))dx but ∫_0 ^1 (e^(−2x) /(1+x)) dx= ∫_0 ^1 e^(−2x) ( Σ_(n0) ^∝ (−1)^n x^n )dx = Σ_(n=0) ^∝ (−1)^n ∫_0 ^1 x^n e^(−2x) dx= Σ_(n=0) ^∝ (−1)^n A_n A_n = ∫_0 ^1 x^n e^(−2x) dx with parts u=x^n and v^, = e^(−2x) A_n = −(1/2)e^(−2x) x^n ]_0 ^(1 ) − ∫_0 ^1 n x^(n−1) (−(1/2) e^(−2x) )dx A_n = −(1/(2e^2 )) +(n/2) A_(n−1) ⇒2A_n = n A_(n−1) −(1/e^2 ) and we find A_n by recurence...be continued.....](https://www.tinkutara.com/question/Q27876.png)
$${let}\:{put}\:{I}=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{−\mathrm{2}{x}} {ln}\left(\mathrm{1}+{x}\right){dx}\:\:{let}\:{integrate}\:{par}\:{parts} \\ $$$${I}=\:\left[\:\frac{−\mathrm{1}}{\mathrm{2}}\:{e}^{−\mathrm{2}{x}} \:{ln}\left(\mathrm{1}+{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{−\mathrm{1}}{\mathrm{2}}\:{e}^{−\mathrm{2}{x}} \:\:\frac{{dx}}{\mathrm{1}+{x}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\:{e}^{−\mathrm{2}} {ln}\left(\mathrm{2}\:\right)\:+\:\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{e}^{−\mathrm{2}{x}} }{\mathrm{1}+{x}}{dx}\:\:{but} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{e}^{−\mathrm{2}{x}} }{\mathrm{1}+{x}}\:{dx}=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{−\mathrm{2}{x}} \left(\:\sum_{{n}\mathrm{0}} ^{\propto} \left(−\mathrm{1}\right)^{{n}} \:{x}^{{n}} \right){dx} \\ $$$$=\:\sum_{{n}=\mathrm{0}} ^{\propto} \:\left(−\mathrm{1}\right)^{{n}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{x}^{{n}} \:{e}^{−\mathrm{2}{x}} {dx}=\:\sum_{{n}=\mathrm{0}} ^{\propto} \left(−\mathrm{1}\right)^{{n}} {A}_{{n}} \\ $$$${A}_{{n}} =\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{n}} {e}^{−\mathrm{2}{x}} {dx}\:\:\:{with}\:{parts}\:{u}={x}^{{n}} \:{and}\:{v}^{,} =\:{e}^{−\mathrm{2}{x}} \\ $$$$\left.{A}_{{n}} =\:−\frac{\mathrm{1}}{\mathrm{2}}{e}^{−\mathrm{2}{x}} {x}^{{n}} \right]_{\mathrm{0}} ^{\mathrm{1}\:} −\:\int_{\mathrm{0}} ^{\mathrm{1}} {n}\:{x}^{{n}−\mathrm{1}} \left(−\frac{\mathrm{1}}{\mathrm{2}}\:{e}^{−\mathrm{2}{x}} \right){dx} \\ $$$${A}_{{n}} =\:−\frac{\mathrm{1}}{\mathrm{2}{e}^{\mathrm{2}} }\:+\frac{{n}}{\mathrm{2}}\:{A}_{{n}−\mathrm{1}} \:\:\Rightarrow\mathrm{2}{A}_{{n}} =\:{n}\:{A}_{{n}−\mathrm{1}} \:\:−\frac{\mathrm{1}}{{e}^{\mathrm{2}} }\:\:\:{and}\:{we}\:{find} \\ $$$${A}_{{n}} \:{by}\:\:{recurence}…{be}\:{continued}….. \\ $$
