Question Number 61453 by maxmathsup by imad last updated on 02/Jun/19
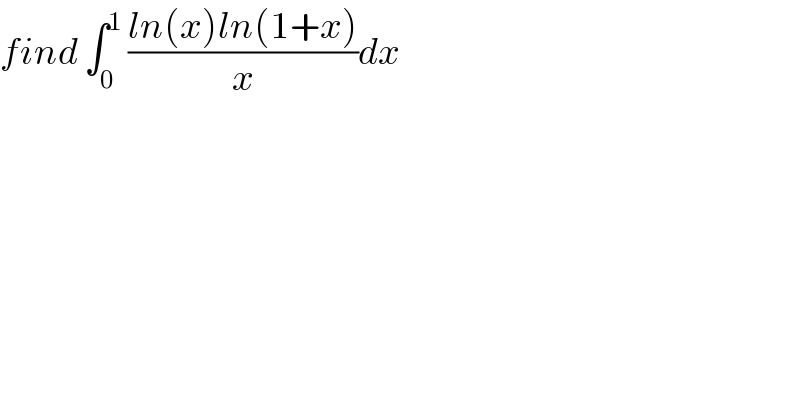
$${find}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left({x}\right){ln}\left(\mathrm{1}+{x}\right)}{{x}}{dx} \\ $$
Answered by Smail last updated on 02/Jun/19
![A=∫_0 ^1 ((ln(x)ln(1+x))/x)dx =∫_0 ^1 ((lnx)/x)Σ_(n=1) ^∞ (((−1)^(n−1) x^n )/n)dx =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)∫_0 ^1 x^(n−1) ln(x)dx By parts u=lnx⇒u′=(1/x) v′=x^(n−1) ⇒v=(x^n /n) A=Σ_(n=1) ^∞ (((−1)^(n−1) )/n)([((x^n ln(x))/n)]_0 ^1 −∫_0 ^1 (x^(n−1) /n)dx) =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)((1/n)[(x^n /n)]_0 ^1 ) =Σ_(n=1) ^∞ (((−1)^(n−1) )/n^3 )=Σ_(n=0) ^∞ (1/((2n+1)^3 ))−Σ_(n=1) ^∞ (1/((2n)^3 )) =Σ_(n=0) ^∞ (1/((2n+1)^3 ))+Σ_(n=1) ^∞ (1/((2n)^3 ))−2Σ_(n=1) ^∞ (1/((2n)^3 )) =Σ_(n=1) ^∞ (1/n^3 )−(2/8)Σ_(n=1) ^∞ (1/n^3 ) =(3/4)Σ_(n=1) ^∞ (1/n^3 ) A=(3/4)ζ(3)≈0.9013](https://www.tinkutara.com/question/Q61462.png)
$${A}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({x}\right){ln}\left(\mathrm{1}+{x}\right)}{{x}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{lnx}}{{x}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {x}^{{n}} }{{n}}{dx} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}−\mathrm{1}} {ln}\left({x}\right){dx} \\ $$$${By}\:{parts} \\ $$$${u}={lnx}\Rightarrow{u}'=\frac{\mathrm{1}}{{x}} \\ $$$${v}'={x}^{{n}−\mathrm{1}} \Rightarrow{v}=\frac{{x}^{{n}} }{{n}} \\ $$$${A}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\left(\left[\frac{{x}^{{n}} {ln}\left({x}\right)}{{n}}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{n}−\mathrm{1}} }{{n}}{dx}\right) \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\left(\frac{\mathrm{1}}{{n}}\left[\frac{{x}^{{n}} }{{n}}\right]_{\mathrm{0}} ^{\mathrm{1}} \right) \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}^{\mathrm{3}} }=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{3}} }−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}\right)^{\mathrm{3}} } \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{3}} }+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}\right)^{\mathrm{3}} }−\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}\right)^{\mathrm{3}} } \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{3}} }−\frac{\mathrm{2}}{\mathrm{8}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{3}} } \\ $$$$=\frac{\mathrm{3}}{\mathrm{4}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{3}} } \\ $$$${A}=\frac{\mathrm{3}}{\mathrm{4}}\zeta\left(\mathrm{3}\right)\approx\mathrm{0}.\mathrm{9013} \\ $$
