Question Number 88033 by M±th+et£s last updated on 07/Apr/20
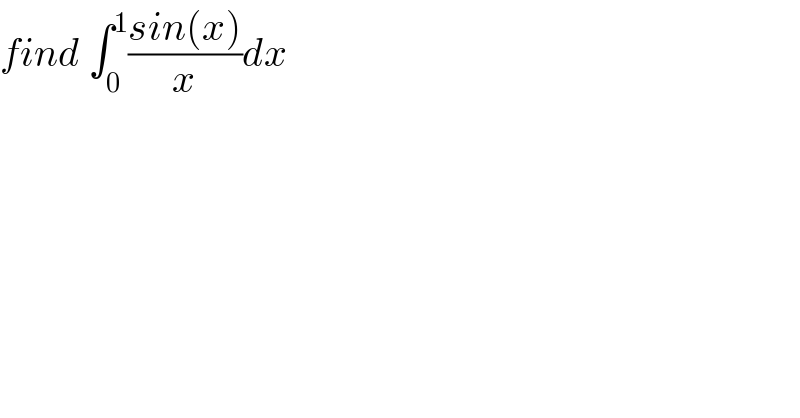
$${find}\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{sin}\left({x}\right)}{{x}}{dx} \\ $$
Commented by mathmax by abdo last updated on 08/Apr/20
![approximate value we have sinx =Σ_(n=0) ^∞ (((−1)^n )/((2n+1)!))x^(2n+1) ⇒ sinx =x−(x^3 /(3!)) +o(x^3 ) ⇒ ∀ x∈[0,1] x−(x^3 /6)≤sinx ≤x ⇒ 1−(x^2 /6)≤((sinx)/x)≤1 ⇒∫_0 ^1 (1−(x^2 /6))dx ≤ ∫_0 ^1 ((sinx)/x)dx ≤1 we have ∫_0 ^1 (1−(x^2 /6))dx =[x−(1/(18))x^3 ]_0 ^1 =1−(1/(18)) =((17)/(18)) ⇒ ((17)/(18))≤ ∫_0 ^1 ((sinx)/x)dx ≤1 we can take v_0 =(1/2) +((17)/(46)) as a apprimate value for this integral I ∼0,5 +0,369 ⇒ I ∼0,869](https://www.tinkutara.com/question/Q88036.png)
$${approximate}\:{value}\:{we}\:{have}\:{sinx}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}{x}^{\mathrm{2}{n}+\mathrm{1}} \:\:\Rightarrow \\ $$$${sinx}\:={x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\:+{o}\left({x}^{\mathrm{3}} \right)\:\Rightarrow\:\forall\:{x}\in\left[\mathrm{0},\mathrm{1}\right]\:\:\:\:\:{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\leqslant{sinx}\:\leqslant{x}\:\Rightarrow \\ $$$$\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}\leqslant\frac{{sinx}}{{x}}\leqslant\mathrm{1}\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}\right){dx}\:\leqslant\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{sinx}}{{x}}{dx}\:\leqslant\mathrm{1} \\ $$$${we}\:{have}\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}\right){dx}\:=\left[{x}−\frac{\mathrm{1}}{\mathrm{18}}{x}^{\mathrm{3}} \right]_{\mathrm{0}} ^{\mathrm{1}} =\mathrm{1}−\frac{\mathrm{1}}{\mathrm{18}}\:=\frac{\mathrm{17}}{\mathrm{18}}\:\Rightarrow \\ $$$$\frac{\mathrm{17}}{\mathrm{18}}\leqslant\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{sinx}}{{x}}{dx}\:\leqslant\mathrm{1}\:\:{we}\:{can}\:{take}\:{v}_{\mathrm{0}} =\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{17}}{\mathrm{46}}\:\:{as}\:{a}\:{apprimate} \\ $$$${value}\:{for}\:{this}\:{integral} \\ $$$${I}\:\sim\mathrm{0},\mathrm{5}\:+\mathrm{0},\mathrm{369}\:\Rightarrow\:{I}\:\sim\mathrm{0},\mathrm{869} \\ $$
Commented by mathmax by abdo last updated on 08/Apr/20
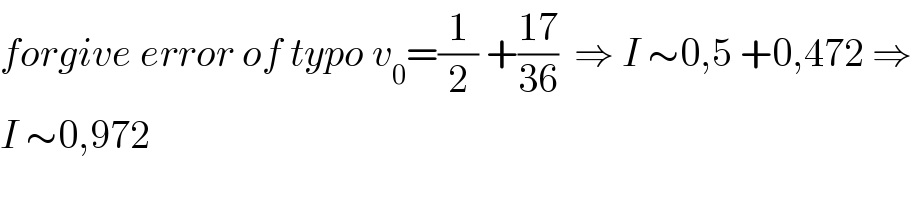
$${forgive}\:{error}\:{of}\:{typo}\:{v}_{\mathrm{0}} =\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{17}}{\mathrm{36}}\:\:\Rightarrow\:{I}\:\sim\mathrm{0},\mathrm{5}\:+\mathrm{0},\mathrm{472}\:\Rightarrow \\ $$$${I}\:\sim\mathrm{0},\mathrm{972} \\ $$
Commented by M±th+et£s last updated on 08/Apr/20

$${thank}\:{you}\:{sir} \\ $$
Commented by abdomathmax last updated on 08/Apr/20

$${you}\:{are}\:{welcome} \\ $$
