Menu Close

find-0-1-x-1-x-lnx-dx-

Tinku Tara 0 Comments
Pin




Question Number 172564 by Mathspace last updated on 28/Jun/22
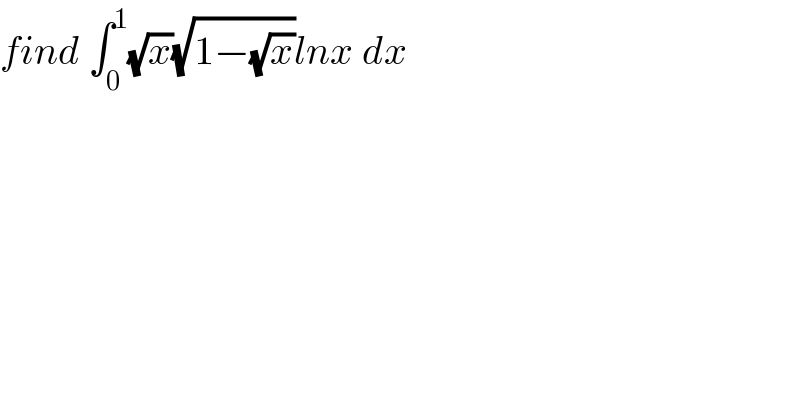
find ∫_0 ^1 (√x)(√(1−(√x)))lnx dx
$${find}\:\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{{x}}\sqrt{\mathrm{1}−\sqrt{{x}}}{lnx}\:{dx} \\ $$
Answered by Ar Brandon last updated on 28/Jun/22
I=∫_0 ^1 (√x)(√(1−(√x)))lnxdx, x=t^2 =4∫_0 ^1 t^2 (√(1−t))lntdt=4(∂/∂α)∣_(α=3) ∫_0 ^1 t^(α−1) (√(1−t))dt =4(∂/∂α)∣_(α=3) β(α, (3/2))=4(∂/∂α)∣_(α=3) ((Γ(α)Γ((3/2)))/(Γ(α+(3/2)))) =2(√π)(∂/∂α)∣_(α=3) ((Γ(α))/(Γ(α+(3/2))))=2(√π)(((Γ′(α))/(Γ(α+(3/2))))−((Γ(α)Γ′(α+(3/2)))/(Γ^2 (α+(3/2)))))_(α=3) =2(√π)(((Γ(3)ψ(3))/(Γ((9/2))))−((Γ(3)Γ((9/2))ψ((9/2)))/(Γ^2 ((9/2))))) =2(√π)(((2((1/2)+1−γ))/((7/2)∙(5/2)∙(3/2)∙(1/2)∙(√π)))−((2((2/7)+(2/5)+(2/3)+2−γ−2ln2))/((7/2)∙(5/2)∙(3/2)∙(1/2)∙(√π)))) =((32)/(105))(3−2γ−((704)/(105))+2γ+4ln2)=((32)/(105))(4ln2−((389)/(105)))
$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{{x}}\sqrt{\mathrm{1}−\sqrt{{x}}}\mathrm{ln}{xdx},\:{x}={t}^{\mathrm{2}} \\ $$$$\:\:\:=\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\mathrm{2}} \sqrt{\mathrm{1}−{t}}\mathrm{ln}{tdt}=\mathrm{4}\frac{\partial}{\partial\alpha}\mid_{\alpha=\mathrm{3}} \int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\alpha−\mathrm{1}} \sqrt{\mathrm{1}−{t}}{dt} \\ $$$$\:\:\:=\mathrm{4}\frac{\partial}{\partial\alpha}\mid_{\alpha=\mathrm{3}} \beta\left(\alpha,\:\frac{\mathrm{3}}{\mathrm{2}}\right)=\mathrm{4}\frac{\partial}{\partial\alpha}\mid_{\alpha=\mathrm{3}} \frac{\Gamma\left(\alpha\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\Gamma\left(\alpha+\frac{\mathrm{3}}{\mathrm{2}}\right)} \\ $$$$\:\:\:=\mathrm{2}\sqrt{\pi}\frac{\partial}{\partial\alpha}\mid_{\alpha=\mathrm{3}} \frac{\Gamma\left(\alpha\right)}{\Gamma\left(\alpha+\frac{\mathrm{3}}{\mathrm{2}}\right)}=\mathrm{2}\sqrt{\pi}\left(\frac{\Gamma'\left(\alpha\right)}{\Gamma\left(\alpha+\frac{\mathrm{3}}{\mathrm{2}}\right)}−\frac{\Gamma\left(\alpha\right)\Gamma'\left(\alpha+\frac{\mathrm{3}}{\mathrm{2}}\right)}{\Gamma^{\mathrm{2}} \left(\alpha+\frac{\mathrm{3}}{\mathrm{2}}\right)}\right)_{\alpha=\mathrm{3}} \\ $$$$\:\:\:=\mathrm{2}\sqrt{\pi}\left(\frac{\Gamma\left(\mathrm{3}\right)\psi\left(\mathrm{3}\right)}{\Gamma\left(\frac{\mathrm{9}}{\mathrm{2}}\right)}−\frac{\Gamma\left(\mathrm{3}\right)\Gamma\left(\frac{\mathrm{9}}{\mathrm{2}}\right)\psi\left(\frac{\mathrm{9}}{\mathrm{2}}\right)}{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{9}}{\mathrm{2}}\right)}\right) \\ $$$$\:\:\:=\mathrm{2}\sqrt{\pi}\left(\frac{\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{1}−\gamma\right)}{\frac{\mathrm{7}}{\mathrm{2}}\centerdot\frac{\mathrm{5}}{\mathrm{2}}\centerdot\frac{\mathrm{3}}{\mathrm{2}}\centerdot\frac{\mathrm{1}}{\mathrm{2}}\centerdot\sqrt{\pi}}−\frac{\mathrm{2}\left(\frac{\mathrm{2}}{\mathrm{7}}+\frac{\mathrm{2}}{\mathrm{5}}+\frac{\mathrm{2}}{\mathrm{3}}+\mathrm{2}−\gamma−\mathrm{2ln2}\right)}{\frac{\mathrm{7}}{\mathrm{2}}\centerdot\frac{\mathrm{5}}{\mathrm{2}}\centerdot\frac{\mathrm{3}}{\mathrm{2}}\centerdot\frac{\mathrm{1}}{\mathrm{2}}\centerdot\sqrt{\pi}}\right) \\ $$$$\:\:\:=\frac{\mathrm{32}}{\mathrm{105}}\left(\mathrm{3}−\mathrm{2}\gamma−\frac{\mathrm{704}}{\mathrm{105}}+\mathrm{2}\gamma+\mathrm{4ln2}\right)=\frac{\mathrm{32}}{\mathrm{105}}\left(\mathrm{4ln2}−\frac{\mathrm{389}}{\mathrm{105}}\right) \\ $$
Answered by Mathspace last updated on 29/Jun/22
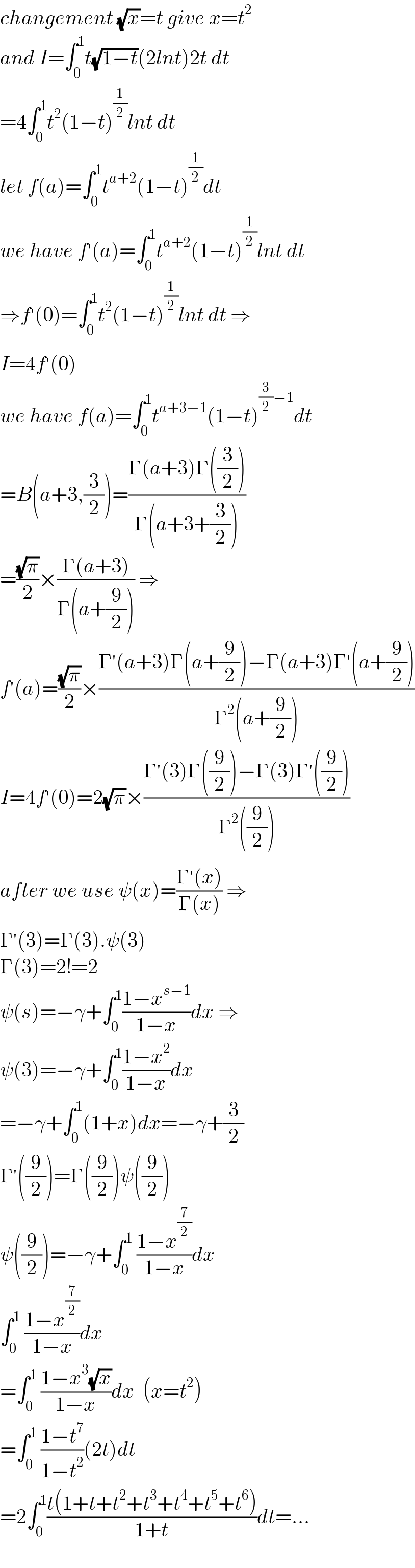
changement (√x)=t give x=t^2 and I=∫_0 ^1 t(√(1−t))(2lnt)2t dt =4∫_0 ^1 t^2 (1−t)^(1/2) lnt dt let f(a)=∫_0 ^1 t^(a+2) (1−t)^(1/2) dt we have f^′ (a)=∫_0 ^1 t^(a+2) (1−t)^(1/2) lnt dt ⇒f^′ (0)=∫_0 ^1 t^2 (1−t)^(1/2) lnt dt ⇒ I=4f^′ (0) we have f(a)=∫_0 ^1 t^(a+3−1) (1−t)^((3/2)−1) dt =B(a+3,(3/2))=((Γ(a+3)Γ((3/2)))/(Γ(a+3+(3/2)))) =((√π)/2)×((Γ(a+3))/(Γ(a+(9/2)))) ⇒ f^′ (a)=((√π)/2)×((Γ^′ (a+3)Γ(a+(9/2))−Γ(a+3)Γ^′ (a+(9/2)))/(Γ^2 (a+(9/2)))) I=4f^′ (0)=2(√π)×((Γ^′ (3)Γ((9/2))−Γ(3)Γ^′ ((9/2)))/(Γ^2 ((9/2)))) after we use ψ(x)=((Γ^′ (x))/(Γ(x))) ⇒ Γ^′ (3)=Γ(3).ψ(3) Γ(3)=2!=2 ψ(s)=−γ+∫_0 ^1 ((1−x^(s−1) )/(1−x))dx ⇒ ψ(3)=−γ+∫_0 ^1 ((1−x^2 )/(1−x))dx =−γ+∫_0 ^1 (1+x)dx=−γ+(3/2) Γ^′ ((9/2))=Γ((9/2))ψ((9/2)) ψ((9/2))=−γ+∫_0 ^1 ((1−x^(7/2) )/(1−x))dx ∫_0 ^1 ((1−x^(7/2) )/(1−x))dx =∫_0 ^1 ((1−x^3 (√x))/(1−x))dx (x=t^2 ) =∫_0 ^1 ((1−t^7 )/(1−t^2 ))(2t)dt =2∫_0 ^1 ((t(1+t+t^2 +t^3 +t^4 +t^5 +t^6 ))/(1+t))dt=...
$${changement}\:\sqrt{{x}}={t}\:{give}\:{x}={t}^{\mathrm{2}} \\ $$$${and}\:{I}=\int_{\mathrm{0}} ^{\mathrm{1}} {t}\sqrt{\mathrm{1}−{t}}\left(\mathrm{2}{lnt}\right)\mathrm{2}{t}\:{dt} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\mathrm{2}} \left(\mathrm{1}−{t}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} {lnt}\:{dt} \\ $$$${let}\:{f}\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{a}+\mathrm{2}} \left(\mathrm{1}−{t}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} {dt} \\ $$$${we}\:{have}\:{f}^{'} \left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{a}+\mathrm{2}} \left(\mathrm{1}−{t}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} {lnt}\:{dt} \\ $$$$\Rightarrow{f}^{'} \left(\mathrm{0}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\mathrm{2}} \left(\mathrm{1}−{t}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} {lnt}\:{dt}\:\Rightarrow \\ $$$${I}=\mathrm{4}{f}^{'} \left(\mathrm{0}\right) \\ $$$${we}\:{have}\:{f}\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{a}+\mathrm{3}−\mathrm{1}} \left(\mathrm{1}−{t}\right)^{\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{1}} {dt} \\ $$$$={B}\left({a}+\mathrm{3},\frac{\mathrm{3}}{\mathrm{2}}\right)=\frac{\Gamma\left({a}+\mathrm{3}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\Gamma\left({a}+\mathrm{3}+\frac{\mathrm{3}}{\mathrm{2}}\right)} \\ $$$$=\frac{\sqrt{\pi}}{\mathrm{2}}×\frac{\Gamma\left({a}+\mathrm{3}\right)}{\Gamma\left({a}+\frac{\mathrm{9}}{\mathrm{2}}\right)}\:\Rightarrow \\ $$$${f}^{'} \left({a}\right)=\frac{\sqrt{\pi}}{\mathrm{2}}×\frac{\Gamma^{'} \left({a}+\mathrm{3}\right)\Gamma\left({a}+\frac{\mathrm{9}}{\mathrm{2}}\right)−\Gamma\left({a}+\mathrm{3}\right)\Gamma^{'} \left({a}+\frac{\mathrm{9}}{\mathrm{2}}\right)}{\Gamma^{\mathrm{2}} \left({a}+\frac{\mathrm{9}}{\mathrm{2}}\right)} \\ $$$${I}=\mathrm{4}{f}^{'} \left(\mathrm{0}\right)=\mathrm{2}\sqrt{\pi}×\frac{\Gamma^{'} \left(\mathrm{3}\right)\Gamma\left(\frac{\mathrm{9}}{\mathrm{2}}\right)−\Gamma\left(\mathrm{3}\right)\Gamma^{'} \left(\frac{\mathrm{9}}{\mathrm{2}}\right)}{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{9}}{\mathrm{2}}\right)} \\ $$$${after}\:{we}\:{use}\:\psi\left({x}\right)=\frac{\Gamma^{'} \left({x}\right)}{\Gamma\left({x}\right)}\:\Rightarrow \\ $$$$\Gamma^{'} \left(\mathrm{3}\right)=\Gamma\left(\mathrm{3}\right).\psi\left(\mathrm{3}\right) \\ $$$$\Gamma\left(\mathrm{3}\right)=\mathrm{2}!=\mathrm{2} \\ $$$$\psi\left({s}\right)=−\gamma+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{x}^{{s}−\mathrm{1}} }{\mathrm{1}−{x}}{dx}\:\Rightarrow \\ $$$$\psi\left(\mathrm{3}\right)=−\gamma+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{1}−{x}}{dx} \\ $$$$=−\gamma+\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+{x}\right){dx}=−\gamma+\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\Gamma^{'} \left(\frac{\mathrm{9}}{\mathrm{2}}\right)=\Gamma\left(\frac{\mathrm{9}}{\mathrm{2}}\right)\psi\left(\frac{\mathrm{9}}{\mathrm{2}}\right) \\ $$$$\psi\left(\frac{\mathrm{9}}{\mathrm{2}}\right)=−\gamma+\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}−{x}^{\frac{\mathrm{7}}{\mathrm{2}}} }{\mathrm{1}−{x}}{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}−{x}^{\frac{\mathrm{7}}{\mathrm{2}}} }{\mathrm{1}−{x}}{dx}\:\: \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}−{x}^{\mathrm{3}} \sqrt{{x}}}{\mathrm{1}−{x}}{dx}\:\:\left({x}={t}^{\mathrm{2}} \right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}−{t}^{\mathrm{7}} }{\mathrm{1}−{t}^{\mathrm{2}} }\left(\mathrm{2}{t}\right){dt} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}\left(\mathrm{1}+{t}+{t}^{\mathrm{2}} +{t}^{\mathrm{3}} +{t}^{\mathrm{4}} +{t}^{\mathrm{5}} +{t}^{\mathrm{6}} \right)}{\mathrm{1}+{t}}{dt}=… \\ $$
Commented by Ar Brandon last updated on 29/Jun/22
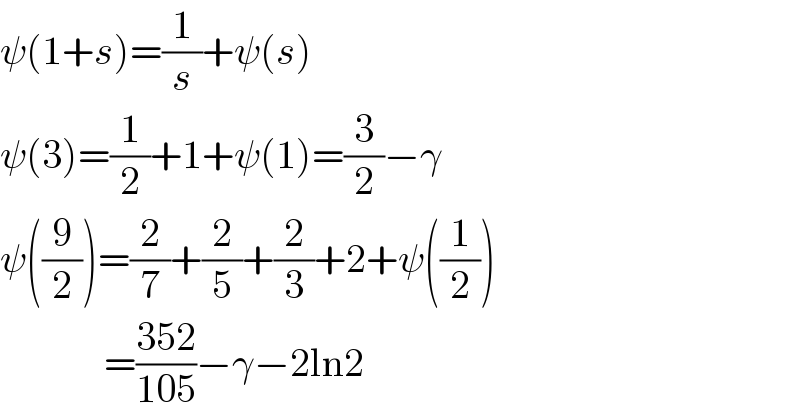
ψ(1+s)=(1/s)+ψ(s) ψ(3)=(1/2)+1+ψ(1)=(3/2)−γ ψ((9/2))=(2/7)+(2/5)+(2/3)+2+ψ((1/2)) =((352)/(105))−γ−2ln2
$$\psi\left(\mathrm{1}+{s}\right)=\frac{\mathrm{1}}{{s}}+\psi\left({s}\right) \\ $$$$\psi\left(\mathrm{3}\right)=\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{1}+\psi\left(\mathrm{1}\right)=\frac{\mathrm{3}}{\mathrm{2}}−\gamma \\ $$$$\psi\left(\frac{\mathrm{9}}{\mathrm{2}}\right)=\frac{\mathrm{2}}{\mathrm{7}}+\frac{\mathrm{2}}{\mathrm{5}}+\frac{\mathrm{2}}{\mathrm{3}}+\mathrm{2}+\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{352}}{\mathrm{105}}−\gamma−\mathrm{2ln2} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *