Question Number 158775 by HongKing last updated on 08/Nov/21
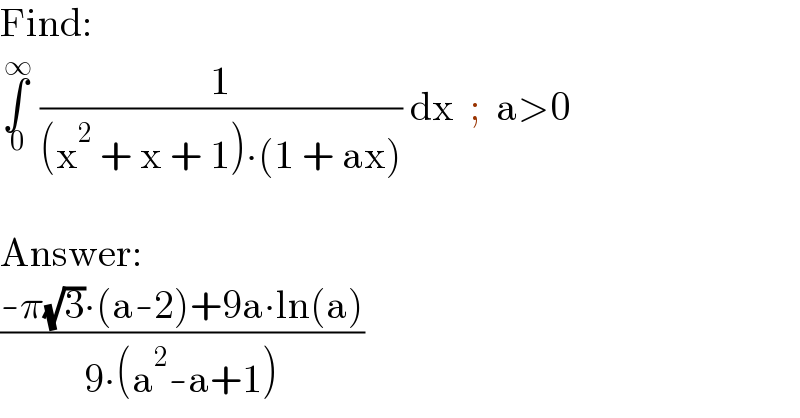
$$\mathrm{Find}: \\ $$$$\underset{\:\mathrm{0}} {\overset{\:\infty} {\int}}\:\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{x}\:+\:\mathrm{1}\right)\centerdot\left(\mathrm{1}\:+\:\mathrm{ax}\right)}\:\mathrm{dx}\:\:;\:\:\mathrm{a}>\mathrm{0} \\ $$$$ \\ $$$$\mathrm{Answer}: \\ $$$$\frac{-\pi\sqrt{\mathrm{3}}\centerdot\left(\mathrm{a}-\mathrm{2}\right)+\mathrm{9a}\centerdot\mathrm{ln}\left(\mathrm{a}\right)}{\mathrm{9}\centerdot\left(\mathrm{a}^{\mathrm{2}} -\mathrm{a}+\mathrm{1}\right)} \\ $$
Answered by MJS_new last updated on 08/Nov/21

$$\int\frac{{dx}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)\left({ax}+\mathrm{1}\right)}= \\ $$$$=\frac{{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} −{a}+\mathrm{1}}\int\frac{{dx}}{{ax}+\mathrm{1}}−\frac{{a}}{{a}^{\mathrm{2}} −{a}+\mathrm{1}}\int\frac{{x}+\frac{{a}−\mathrm{1}}{{a}}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx}= \\ $$$$=\frac{{a}}{{a}^{\mathrm{2}} −{a}+\mathrm{1}}\mathrm{ln}\:\mid{ax}+\mathrm{1}\mid\:−\frac{\left({a}−\mathrm{2}\right)}{\:\sqrt{\mathrm{3}}\left({a}^{\mathrm{2}} −{a}+\mathrm{1}\right)}\mathrm{arctan}\:\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:−\frac{{a}}{\mathrm{2}\left({a}^{\mathrm{2}} −{a}+\mathrm{1}\right)}\mathrm{ln}\:\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)\:= \\ $$$$=\frac{{a}}{\mathrm{2}\left({a}^{\mathrm{2}} −{a}+\mathrm{1}\right)}\mathrm{ln}\:\frac{\left({ax}+\mathrm{1}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\:−\frac{\left({a}−\mathrm{2}\right)}{\:\sqrt{\mathrm{3}}\left({a}^{\mathrm{2}} −{a}+\mathrm{1}\right)}\mathrm{arctan}\:\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:+{C} \\ $$$$\Rightarrow \\ $$$$\mathrm{answer}\:\mathrm{is} \\ $$$$\frac{\mathrm{9}{a}\mathrm{ln}\:{a}\:−\left({a}−\mathrm{2}\right)\pi\sqrt{\mathrm{3}}}{\mathrm{9}\left({a}^{\mathrm{2}} −{a}+\mathrm{1}\right)} \\ $$
Commented by HongKing last updated on 09/Nov/21

$$\mathrm{peefet}\:\mathrm{my}\:\mathrm{dear}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$
